Machine Learning Concepts (Part 3)

Content

  1. Content
  2. Model Evaluation
  3. What is inductive bias, selection bias, statistical bias?
  4. What is the difference between inductive machine learning and deductive machine learning?
  5. How will you know which machine learning algorithm to choose for your classification problem?
  6. Advantages of some particular algorithms
    1. Naive Bayes
    2. Logistic Regression
    3. Decision Tree
    4. SVM
  7. Time complexity of decision tree algorithm
    1. Time Complexity for Decision Tree construction
  8. Bias and Variance Tradeoff
    1. Different types of Bias in ML?
    2. Why do we need/want the bias term?
  9. Different types of models and their example
  10. How to seed K-means clustering algorithm?
  11. The BLAS library and how does it work? what are the other option?
  12. What areas of machine learning are you most familiar with?
  13. Tell about positives and negatives of using Gaussian processes / general kernel methods approach to learning.
    1. How does a kernel method scale with the number of instances (e.g. with a Gaussian rbf kernel)?
    2. Describe ways to overcome scaling issues.
  14. What are some tools for parallelizing machine learning algorithms?
  15. In Python, do you have a favorite/least favorite PEP?
  16. Explain the tradeoff between bias and variance in a regression problem.
  17. Exercise
    1. Distributed systems
    2. Experience based question (hands-on experience, past accomplishments, etc.):
  18. Question and Answer
  19. Question and Answer on R
  20. Question and Answer on Python
  21. Question Source

Model Evaluation

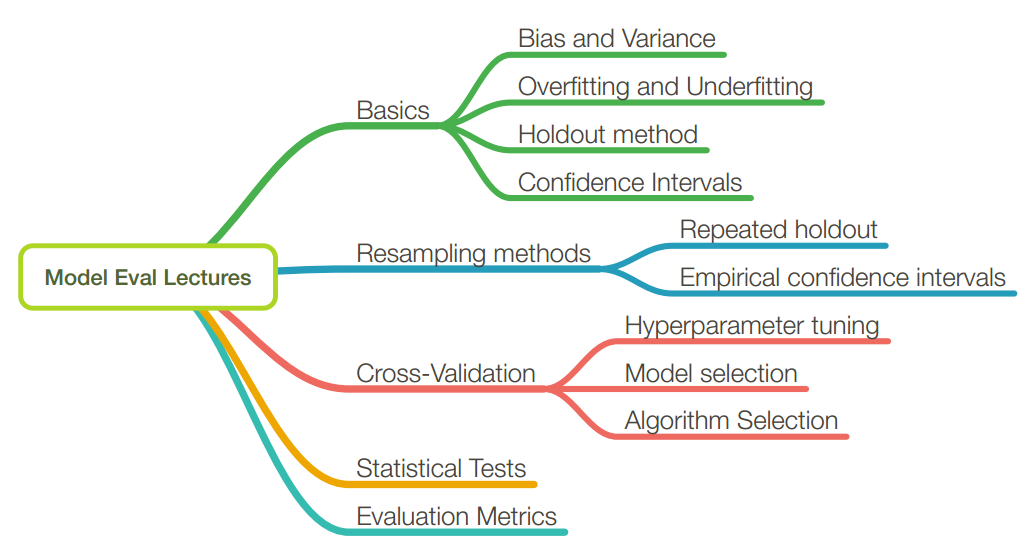
* image source (slide 8)

Reference:

Content

What is inductive bias, selection bias, statistical bias?

Inductive bias is the set of assumptions a learner uses to predict results given inputs it has not yet encountered.

  • Generally speaking, the closer your assumptions are to reality the better your results will be. Additionally, more and stronger assumptions tend to make solving problems easier. If an assumption is correct then it’s always helpful to use it. However, it’s also common to assume things that obviously aren’t true because they’re practical. Every machine learning algorithm has some sort of inductive bias, and it’s those underlying assumptions you may not even realize you’re making that determine how well your algorithms are going to work in practice.
  • Let’s suppose you don’t know anything about swans. You decide to visit Swan River in Australia. You see a swan for the first time, and that swan is black. What color will the next Swan you see be? Black seems like a pretty good guess. It’s not a logical guess, but given what we know, black is a better guess than anything else.

Selection bias is the bias introduced by the selection of individuals, groups or data for analysis in such a way that proper randomization is not achieved, thereby ensuring that the sample obtained is not representative of the population intended to be analyzed.[1] It is sometimes referred to as the selection effect. The phrase “selection bias” most often refers to the distortion of a statistical analysis, resulting from the method of collecting samples. If the selection bias is not taken into account, then some conclusions of the study may not be accurate. Example: Sampling Bias

Sampling Bias: It is systematic error due to a non-random sample of a population,causing some members of the population to be less likely to be included than others, resulting in a biased sample, defined as a statistical sample of a population (or non-human factors) in which all participants are not equally balanced or objectively represented. It is mostly classified as a subtype of selection bias.

Statistical Bias: For a point estimator, statistical bias is defined as the difference between the parameter to be estimated and the mathematical expectation of the estimator.

Reference

Content

What is the difference between inductive machine learning and deductive machine learning?

Inductive Learning: We are given input samples $(x)$ and output samples $(f(x))$ and the problem is to estimate the function $(f)$. Specifically, the problem is to generalize from the samples and the mapping to be useful to estimate the output for new samples in the future. source

Content

How will you know which machine learning algorithm to choose for your classification problem?

If your training set is small, high bias/low variance classifiers (e.g., Naive Bayes) have an advantage over low bias/high variance classifiers (e.g., kNN), since the latter will overfit. But low bias/high variance classifiers start to win out as your training set grows (they have lower asymptotic error), since high bias classifiers aren’t powerful enough to provide accurate models.

Content

Advantages of some particular algorithms

Naive Bayes

Advantages of Naive Bayes: Super simple, you’re just doing a bunch of counts. If the NB conditional independence assumption actually holds, a Naive Bayes classifier will converge quicker than discriminative models like logistic regression, so you need less training data. And even if the NB assumption doesn’t hold, a NB classifier still often does a great job in practice. A good bet if want something fast and easy that performs pretty well.

  • Main Disadvantage is that it can’t learn interactions between features (e.g., it can’t learn that although you love movies with Brad Pitt and Tom Cruise, you hate movies where they’re together).

Logistic Regression

Advantages:

  • Lots of ways to regularize your model, and you don’t have to worry as much about your features being correlated, like you do in Naive Bayes.
  • You also have a nice probabilistic interpretation, unlike decision trees or SVMs, and you can easily update your model to take in new data (using an online gradient descent method).
  • Use it if you want a probabilistic framework (e.g., to easily adjust classification thresholds, to say when you’re unsure, or to get confidence intervals) or if you expect to receive more training data in the future that you want to be able to quickly incorporate into your model.

Disadvantages:

  1. Main limitation of Logistic Regression is the assumption of linearity between the dependent variable and the independent variables. In the real world, the data is rarely linearly separable. Most of the time data would be a jumbled mess.

  2. If the number of observations are lesser than the number of features, Logistic Regression should not be used, otherwise it may lead to overfit.

  3. Logistic Regression can only be used to predict discrete functions. Therefore, the dependent variable of Logistic Regression is restricted to the discrete number set. This restriction itself is problematic, as it is prohibitive to the prediction of continuous data.

Decision Tree

Advantages:

  • Easy to interpret and explain (for some people – I’m not sure I fall into this camp). They easily handle feature interactions and they’re non-parametric, so you don’t have to worry about outliers or whether the data is linearly separable (e.g., decision trees easily take care of cases where you have class A at the low end of some feature x, class B in the mid-range of feature x, and A again at the high end).

Disadvantages:

  • They don’t support online learning, so you have to rebuild your tree when new examples come on.
  • Another disadvantage is that they easily overfit, but that’s where ensemble methods like random forests (or boosted trees) come in. Plus, random forests are often the winner for lots of problems in classification (usually slightly ahead of SVMs, I believe), they’re fast and scalable, and you don’t have to worry about tuning a bunch of parameters like you do with SVMs, so they seem to be quite popular these days.

SVM

Advantages:

  • High accuracy, nice theoretical guarantees regarding overfitting, and with an appropriate kernel they can work well even if you’re data isn’t linearly separable in the base feature space. Especially popular in text classification problems where very high-dimensional spaces are the norm.
  • Using Kernel trick can be applied to Non-Linear data

Disadvantages:

Memory-intensive, hard to interpret, and kind of annoying to run and tune, though, so I think random forests are starting to steal the crown.

Refrence:

Content

Time complexity of decision tree algorithm

Measuring the time complexity of decision tree algorithms can be complicated, and the approach is not very straight-forward.However, we can make a few simplifying assumption to analyze the complexity of decision trees.

  • Assumption: A decision tree is a balanced binary decision tree,
  • Tree Depth: the final tree will have a depth of $\log_2n$, where $n$ is the number of examples in the training set.
  • Time Complexity for Prediction: $O(\log n)$ (traverse from root to leaf with max height $\log n$)

Time Complexity for Decision Tree construction

The runtime of the decision tree construction is generally $O(mn^2 \log n)$

:atom_symbol: It can be shown that optimal binary split on continuous features is on the boundary between adjacent examples with different class labels. This means that sorting the values of continuous features helps with determining a decision threshold efficiently. If we have $n$ examples, the sorting has time complexity $O(n \log n)$. If we have to compare sort $m$ features, this becomes $O(mn \log n)$

:atom_symbol: To see why the time complexity of decision tree construction is typically quoted at $O(mn^2 \log n)$, keep in mind that we earlier determined the depth of a decision tree at $\log_2 n$. It follows that the number of terminal nodes (leaf nodes) is $2^{\log_2 n}=n$. The total number of nodes in the tree is $2n−1$, and consequently, the number of splitting nodes (non-leaf nodes) in the tree is $2n−1−n=n−1$ (all nodes minus the terminal (leaf) nodes)

Hence, if we are not efficient and resort the features prior to each split we have to perform the $O(mn \log n)$ sorting step up to $\frac{n}{2}$ times – once for each splitting node in the tree – which results in a time complexity of $O(mn^2 \log n)$ .

:zap: Note: Many implementations such as scikit-learn use efficient caching tricks to keep track of the general order of indices at each node such that the features do not need to be re-sorted ateach node; hence, the time complexity of these implementations is just $O(mn \log (n))$.

Reference:

Content

Bias and Variance Tradeoff

Bias: Bias is the difference between the average prediction of our model and the correct value which we are trying to predict.

Variance: Variance is the variability of model prediction for a given data point or a value which tells us spread of our data. Model with high variance pays a lot of attention to training data and does not generalize on the data which it hasn’t seen before.

Mathematically:

Let the variable we are trying to predict as Y and other covariates as X. We assume there is a relationship between the two such that

$Y = f(X) + error$

So the expected squared error at a point x is

$Err(x) = E[(Y - \hat f(x))^2]$
$Err(x)=(E[\hat f(x)]-f(x))^2 + E[(\hat f(x) - E[\hat f(x)])^2] + \sigma_e^2$
$Err(x)=Bias^2 + Variance + Irreducible error$

In the above diagram, center of the target is a model that perfectly predicts correct values. As we move away from the bulls-eye our predictions become get worse and worse.

In supervised learning, underfitting happens when a model unable to capture the underlying pattern of the data. These models usually have high bias and low variance. It happens when we have very less amount of data to build an accurate model or when we try to build a linear model with a nonlinear data. Also, these kind of models are very simple to capture the complex patterns in data like Linear and logistic regression.

In supervised learning, overfitting happens when our model captures the noise along with the underlying pattern in data. It happens when we train our model a lot over noisy dataset. These models have low bias and high variance. These models are very complex like Decision trees which are prone to overfitting.

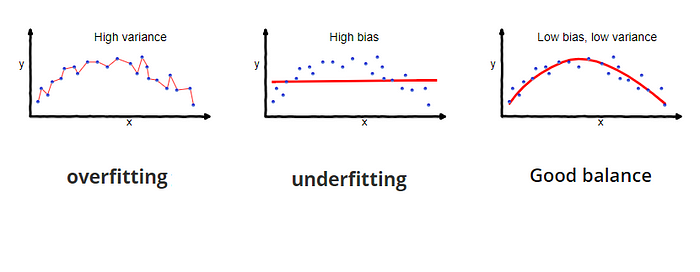
image

  • If our model is too simple and has very few parameters then it may have high bias and low variance.
  • On the other hand if our model has large number of parameters then it’s going to have high variance and low bias.
  • So we need to find the right/good balance without overfitting and underfitting the data.

image

Reference:

Content

Different types of Bias in ML?

Why do we need/want the bias term?

In linear regression, without the bias term your solution has to go through the origin. That is, when all of your features are zero, your predicted value would also have to be zero. However, that may not be the answer the training data suggests. Adding a bias weight that does not depend on any of the features allows the hyperplane described by your learned weights to more easily fit data that doesn’t pass through the origin.

Reference:

Content

Different types of models and their example

  • Parametric Model: A parametric modelis one that can be parametrized by a finite number of parameters
  • Non-Parametric Model: A nonparametric modelis one which cannot be parametrized by a fixed number of parameters.
  • Low-bias High-Variance Model
  • High-Biad Low-Variance Model

Reference:

Content

How to seed K-means clustering algorithm?

  • Important: seeding means, how to initialize the first k centres? Use the algorithm K-Means++. [link]

Content

The BLAS library and how does it work? what are the other option?

Basic Linear Algebra Subprograms (BLAS) is a specification that prescribes a set of low-level routines for performing common linear algebra operations such as vector addition, scalar multiplication, dot products, linear combinations, and matrix multiplication. They are the de facto standard low-level routines for linear algebra libraries; the routines have bindings for both C and Fortran. Although the BLAS specification is general, BLAS implementations are often optimized for speed on a particular machine, so using them can bring substantial performance benefits. BLAS implementations will take advantage of special floating point hardware such as vector registers or SIMD instructions. (wiki)

Alternative to BLAS is LAPACK or ATLAS.

Reference:

What areas of machine learning are you most familiar with?

Very generic Qusestion. Prepare well.

  • Supervised learning
  • Unsupervised learning
  • Anomaly Detection
  • Active Learning
  • Bandits:
    • In the multi-armed bandit problem, at each stage, an agent (or decision maker) chooses one action (or arm), and receives a reward from it. The agent aims at maximizing his rewards. Since he does not know the process generating the rewards, he needs to explore (try) the different actions and yet, exploit (concentrate its draws on) the seemingly most rewarding arms. The bandit problem has been increasingly popular in the machine learning community.
    • It can be a central building block of larger systems, like in evolutionary programming and reinforcement learning, in particular in large state space Markovian Decision Problems. ((ICML Tutorial)[https://sites.google.com/site/banditstutorial/])
  • Gaussian Processes
  • Kernel Methods
  • Deep Networks

Content

Tell about positives and negatives of using Gaussian processes / general kernel methods approach to learning.

  • Positives - non-linear, non-parametric. Negatives - bad scaling with instances, need to do hyper-parameter tuning

How does a kernel method scale with the number of instances (e.g. with a Gaussian rbf kernel)?

  • Quadratic (referring to construction of the gram (kernel) matrix), cubic (referring to the matrix inversion)

Describe ways to overcome scaling issues.

  • nystrom methods/low-rank kernel matrix approximations, random features, local by query/near neighbors

What are some tools for parallelizing machine learning algorithms?

  • GPUs, Matlab parfor, write your own using low level primitives/RPC/MPI, mapreduce, spark, vowpal, graphlab, giraph, petuum, parameterserver

In Python, do you have a favorite/least favorite PEP?

  • Peps are python enhancement proposal. If you have a favorite or least favorite, it means they have knowledge of Python. Follow PEP8

Content

Explain the tradeoff between bias and variance in a regression problem.

In regression, the expected mean squared error of an estimator can be decomposed in terms of bias, variance and noise.

  • On average over datasets of the regression problem, the bias term measures the average amount by which the predictions of the estimator differ from the predictions of the best possible estimator for the problem (i.e., the Bayes model).

  • The variance term measures the variability of the predictions of the estimator when fit over different instances LS of the problem. Finally, the noise measures the irreducible part of the error which is due the variability in the data.

  • Bias: It represents the extent to which the average prediction over all the datasets differs from the desired regression function.
  • Variance: It measures the extent to which the solution to the particular datasets vary around their average, and hence it measures the extent to which the learnt function is sensitive to the particular choice of data. [source, Bishop book, p149]
$Err(x) = E\left[(Y-\hat{f}(x))^2\right]$

Then we can write

$Err(x) = \left(E[\hat{f}(x)]-f(x)\right)^2 + E\left[\left(\hat{f}(x)-E[\hat{f}(x)]\right)^2\right] +\sigma_e^2$
$Err(x) = \mathrm{Bias}^2 + \mathrm{Variance} + \mathrm{Irreducible\ Error}$

Reference:

Content

Exercise

  1. Mention the difference between Data Mining and Machine learning?
  2. Is rotation necessary in PCA? If yes, Why? What will happen if you dont rotate the components?
  3. You are given a data set. The data set has missing values which spread along 1 standard deviation from the median. What percentage of data would remain unaffected? Why?
  4. Why is Naive Bayes machine learning algorithm nave?
  5. How will you explain machine learning in to a layperson?
  6. What is inductive machine learning?
  7. What are the different Algorithm techniques in Machine Learning?
  8. List out some important methods of reducing dimensionality.
  9. Explain prior probability, likelihood and marginal likelihood in context of naive Bayes algorithm?
  10. What are the three stages to build the hypotheses or model in machine learning?
  11. What is the standard approach to supervised learning?
  12. What is Training set and Test set?
  13. List down various approaches for machine learning?
  14. How to know that your model is suffering from low bias and high variance. Which algorithm should you use to tackle it? Why?
  15. How is kNN different from kmeans clustering?
  16. Name some feature extraction techniques used for dimensionality reduction.
  17. List some use cases where classification machine learning algorithms can be used.
  18. What kind of problems does regularization solve?
  19. How much data will you allocate for your training, validation and test sets?
  20. Which one would you prefer to choose model accuracy or model performance?
  21. What is the most frequent metric to assess model accuracy for classification problems?
  22. Describe some popular machine learning methods.
  23. What is not Machine Learning?
  24. Explain what is the function of Unsupervised Learning?
  25. When will you use classification over regression?
  26. How will you differentiate between supervised and unsupervised learning? Give few examples of algorithms for supervised learning?
  27. What is linear regression? Why is it called linear?
  28. How does the variance of the error term change with the number of predictors, in OLS?
  29. Do we always need the intercept term? When do we need it and when do we not?
  30. How interpretable is the given machine learning model?
  31. What will you do if training results in very low accuracy?
  32. Does the developed machine learning model have convergence problems?
  33. Which tools and environments have you used to train and assess machine learning models?
  34. How will you apply machine learning to images?
  35. What is collinearity and what to do with it?
  36. How to remove multicollinearity?
  37. What is overfitting a regression model? What are ways to avoid it?
  38. What is loss function in a Neural Network?
  39. Explain the difference between MLE and MAP inference.
  40. What is boosting?
  41. If the gradient descent does not converge, what could be the problem?
  42. How will you check for a valid binary search tree?
  43. How to check if the regression model fits the data well?
  44. Describe some of the different splitting rules used by different decision tree algorithms.

Distributed systems

  1. Discuss MapReduce (or your favorite parallelization abstraction). Why is MapReduce referred to as a “shared-nothing” architecture (clearly the nodes have to share something, no?) What are the advantages/disadvantages of “shared-nothing”?
  2. Pick an algorithm. Write the pseudo-code for its parallel version.
  3. What are the trade-offs between closed-form and iterative implementations of an algorithm, in the context of distributed systems?

Experience based question (hands-on experience, past accomplishments, etc.):

  1. Do you have experience with R (or Weka, Scikit-learn, SAS, Spark, etc.)? Tell me what you’ve done with that. Write some example data pipelines in that environment.
  2. Tell me about a time when you … { worked on a project involving ML ; optimized an algorithm for performance/accuracy/etc. }
  3. Estimate the amount of time in your past project spent on each segment of your data mining/machine learning work.

Question and Answer

  1. link1
  2. link2
  3. link3

Question and Answer on R

  1. link1
  2. link2
  3. link3

Question and Answer on Python

  1. link1
  2. link2
  3. link3
  4. link4
  5. link5

Question Source

Back to Top

Published on July 6, 2019