Probabilistic and Bayesian Machine Learning
Content
Probabilistic Machine Learning
Bayesian Machine Learning
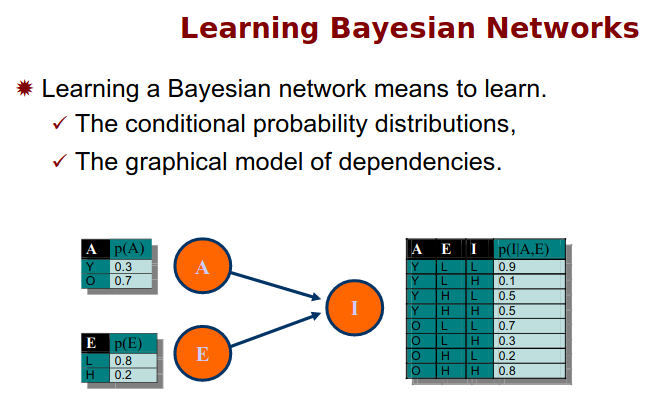
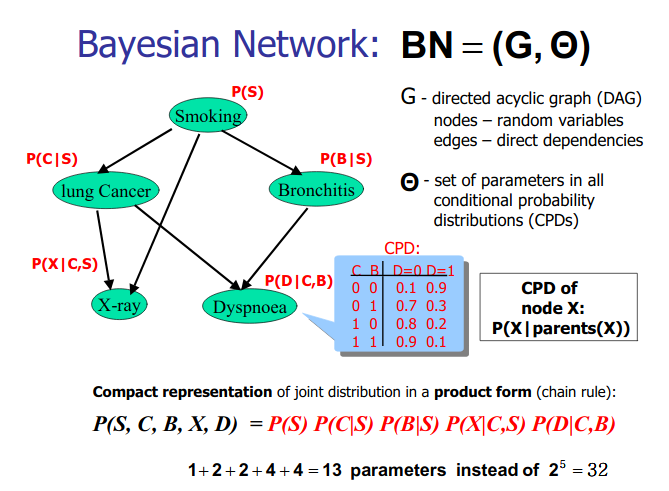
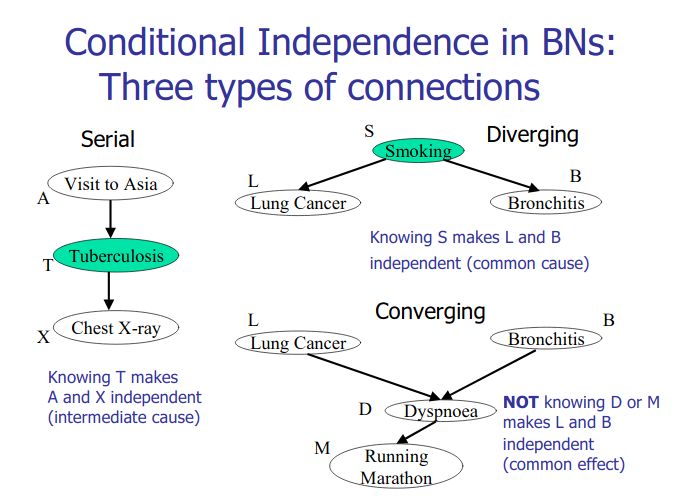
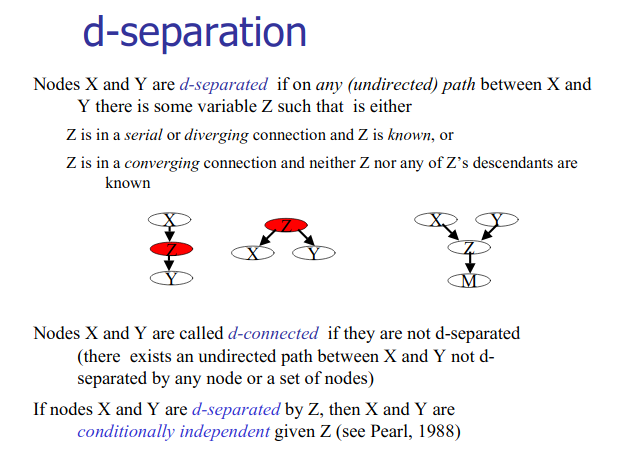
Bayesian Network Learning

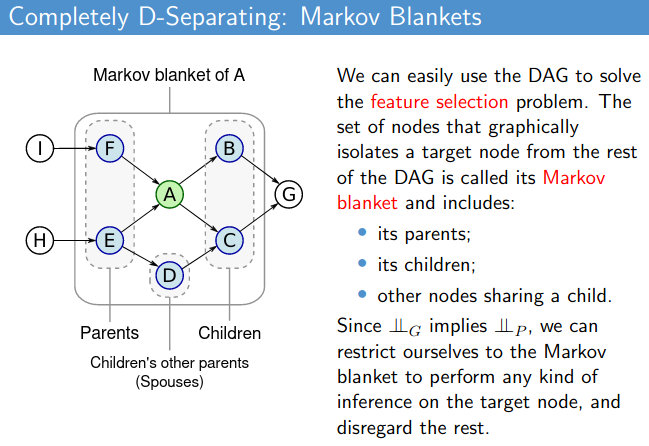
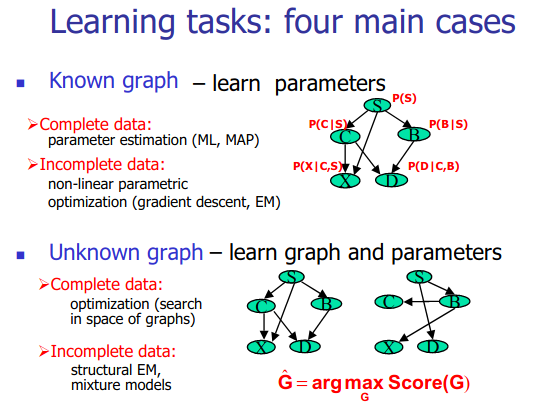
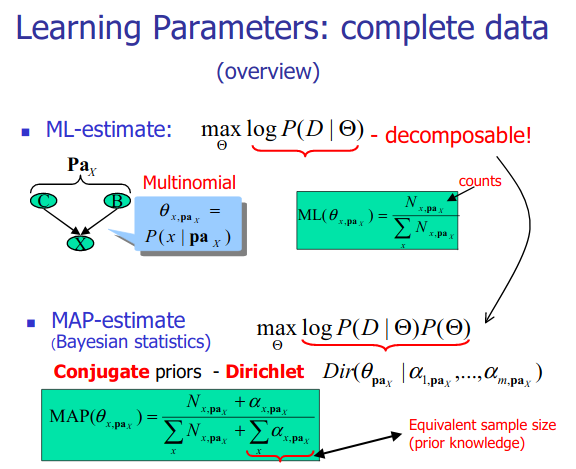
Structure learning for bayesian networks
According to this blog
The task of structure learning for Bayesian networks refers to learn the structure of the directed acyclic graph (DAG) from data. There are two major approaches for the structure learning: score-based approach and constraint-based approach .
Score-based approach
- The score-based approach first defines a criterion to evaluate how well the Bayesian network fits the data, then searches over the space of DAGs for a structure with maximal score.
- In this way, the score-based approach is essentially a search problem and consists of two parts: the definition of score metric and the search algorithm.
Score metrics
The score metrics for a structure $\mathcal{G}$ and data $D$ can be generally defined as:
Here $LL(G:D)$ refers to the log-likelihood of the data under the graph structure $\mathcal{G}$. The parameters in Bayesian network $G$ are estimated based on MLE and the log-likelihood score is calculated based on the estimated parameters. If we consider only the log-likelihood in the score function, we will end up with an overfitting structure (namely, a complete graph.) That is why we have the second term in the scoring function. $\vert D \vert$ is the number of sample and $\vert \vert G \vert \vert$ is the number of parameters in the graph $\mathcal{G}$. With this extra term, we will penalize the over-complicated graph structure and avoid overfitting.
Search algorithms
The most common choice for search algorithms are local search and greedy search.
For local search algorithm, it starts with an empty graph or a complete graph. At each step, it attempts to change the graph structure by a single operation of adding an edge, removing an edge or reversing an edge. (Of course, the operation should preserve the acyclic property.) If the score increases, then it adopts the attempt and does the change, otherwise it makes another attempt.
Implementation
> library(bnlearn)
> data(learning.test)
> pdag = iamb(learning.test)
> pdag
# Bayesian network learned via Constraint-based methods
# model:
# [partially directed graph]
# nodes: 6
# arcs: 5
# undirected arcs: 1
# directed arcs: 4
# average markov blanket size: 2.33
# average neighbourhood size: 1.67
# average branching factor: 0.67
# learning algorithm: IAMB
# conditional independence test: Mutual Information (disc.)
# alpha threshold: 0.05
# tests used in the learning procedure: 134
As we can see from the output above, there is a single undirected arc in pdag; IAMB was not able to set its orientation because its two possible direction are score equivalent.
> score(set.arc(pdag, from = "A", to = "B"), learning.test)
# [1] -24006.73
> score(set.arc(pdag, from = "B", to = "A"), learning.test)
# [1] -24006.73
Fitting the parameters (Maximum Likelihood estimates)
Discrete data
Now that the Bayesian network structure is completely directed, we can fit the parameters of the local distributions, which take the form of conditional probability tables.
> fit = bn.fit(dag, learning.test)
> fit
# Bayesian network parameters
# Parameters of node A (multinomial distribution)
#Conditional probability table:
# a b c
# 0.334 0.334 0.332
# Parameters of node B (multinomial distribution)
#Conditional probability table:
# A
# B a b c
# a 0.8561 0.4449 0.1149
# b 0.0252 0.2210 0.0945
# c 0.1187 0.3341 0.7906
# ...
Reference: