Content

• You can find part 2 here

1. Content
2. Master Theorem
3. Practice followup questions for each coding questions
4. Understand Heap
   1. Representation:
   2. How to build heap
   3. Application of Heap (Priority Queue)
   4. Python Implementation
      1. TODO:
5. Quick Select
6. Leetcode: 221. Maximal Square
7. Difference between bounded and unbounded 0/1 knapsack
   1. In Recursive Approach
   2. In Bottom-Up Approach
8. How to Visualize DP Bototm Up for Longest Palindromic Substring or Subsequence
9. Difference between Longest Palindromic Substring and Longest Palindromic Subsequence
   1. Longest Palindromic Subsequence
   2. Longest Palindromic Substring
10. Spiral Matrix
11. Search in Rotated Sorted Array
12. Comprehensive Data Structure and Algorithm Study Guide
13. Leetcode 210: Course Schedule
14. Kadane Algorithm
    1. Similar question:
    2. Why this problem is important?
15. Best Time to Buy and Sell Stock
16. LC79. Word Search
17. Construct binary tree from tree traversal
    1. from inorder and postorder traversal
    2. from inorder and preorder traversal
18. Interesting problems:
19. Backtracking patterns and variations
    1. Find Permutation
    2. Combination sum
    3. General Strategy:
    4. 
20. Exercise:

• You can access more content on Crack the Code at my other scribe channel.

Master Theorem

*In case the above link is broken, click here

Practice followup questions for each coding questions

1. How do you test your solution? Testing is also an important area in interview and you can treat the interview question as a real life project and how can you guarantee the system works as intended?
2. What if the input size is too large to put in memory?
3. How do you refine your solution and analyze the efficiency?
4. What if the input size is too large to put in disk? How do you solve the scalability issue?
5. What if you have infinite amount of memory? Any way to make the solution faster?
6. You can also try to change some restriction of the question, like what if it’s a normal tree instead of binary tree? What if you can store the dictionary in any data structure you like?

Understand Heap

• A heap is one common implementation of a priority queue.
• A heap is one of the tree structures and represented as a binary tree.

Representation:

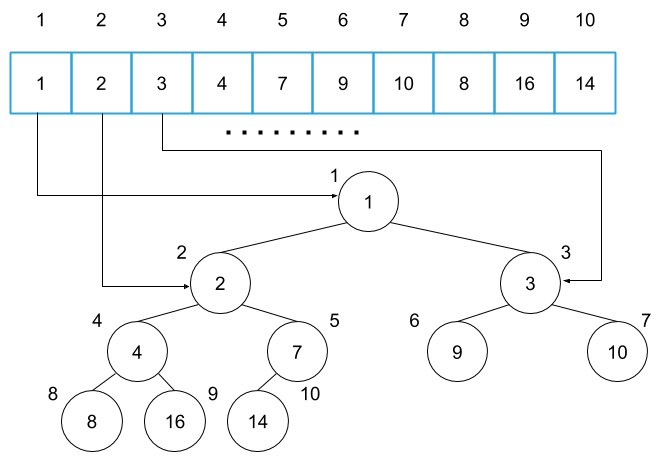
• The heap above is called a min heap, and each value of nodes is less than or equal to the value of child nodes. We call this condition the heap property.

• In a min heap, when you look at the parent node and its child nodes, the parent node always has the smallest value. When a heap has an opposite definition, we call it a max heap. For the following discussions, we call a min heap a heap.

    A root node｜i = 1, the first item of the array
    A parent node｜parent(i) = i / 2
    A left child node｜left(i) = 2i
    A right child node｜right(i)=2i+1

• When you look at the node of index 4, the relation of nodes in the tree corresponds to the indices of the array below.

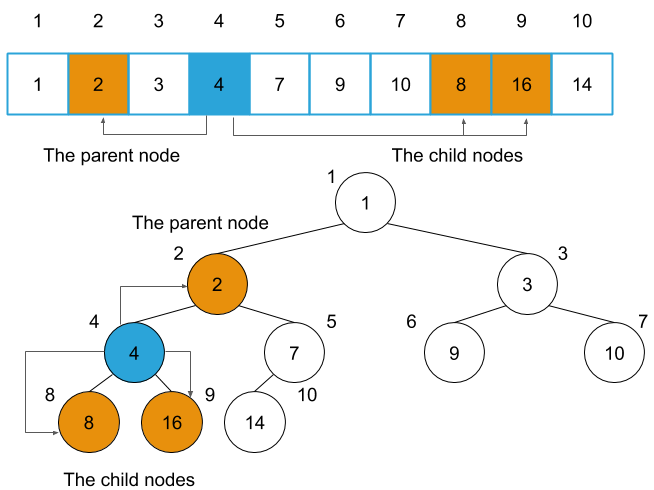
How to build heap

• min_heapify: make some node and its descendant nodes meet the heap property.

Click here for the code.

def min_heapify(array, i):
    left = 2 * i + 1
    right = 2 * i + 2
    length = len(array) - 1
    smallest = i    
    if left <= length and array[i] > array[left]:
        smallest = left
    if right <= length and array[smallest] > array[right]:
        smallest = right
    if smallest != i:
        array[i], array[smallest] = array[smallest], array[i]
        min_heapify(array, smallest)

• First, this method computes the node of the smallest value among the node of index i and its child nodes and then exchange the node of the smallest value with the node of index i.
• When the exchange happens, this method applies min_heapify to the node exchanged.

Index of a list (an array) in Python starts from 0, the way to access the nodes will change as follow.

    The root node｜i = 0
    The parent node｜parent(i) = (i-1) / 2
    The left child node｜left(i) = 2i + 1
    The right child node｜right(i)=2i+2

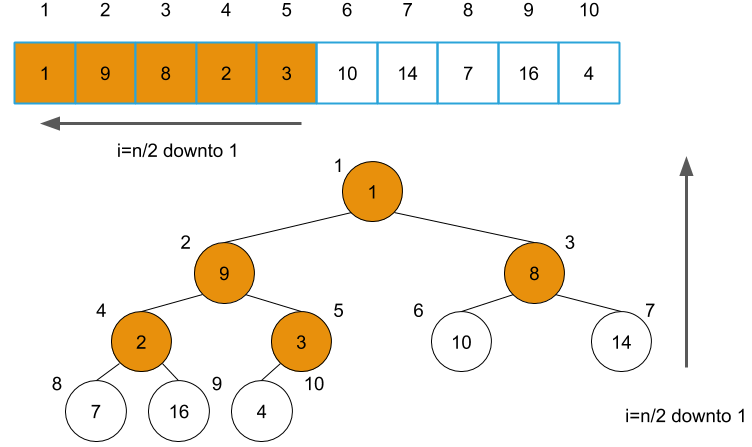
• build_min_heap: produce a heap from an arbitrary array.

def build_min_heap(array):
    #for i=n/2 downto 1
    for i in reversed(range(len(array)//2)):
        min_heapify(array, i)

This function iterates the nodes except the leaf nodes with the for-loop and applies min_heapify to each node. We don’t need to apply min_heapify to the items of indices after n/2+1, which are all the leaf nodes. We apply min_heapify in the orange nodes below.

Application of Heap (Priority Queue)

Applications of Heaps:

1. Heap Sort: Heap Sort uses Binary Heap to sort an array in O(nLogn) time.

2. Priority Queue: Priority queues can be efficiently implemented using Binary Heap because it supports insert(), delete() and extractmax(), decreaseKey() operations in O(logn) time. Binomoial Heap and Fibonacci Heap are variations of Binary Heap. These variations perform union also efficiently.

3. Graph Algorithms: The priority queues are especially used in Graph Algorithms like Dijkstra’s Shortest Path and Prim’s Minimum Spanning Tree.

4. Many problems can be efficiently solved using Heaps. See following for example.

   1. K’th Largest Element in an array.
      1. Sol 1: Create a max heap of size k and return the root
      2. Sol 2: Create a regular max heap and pop/delete items k time
      3. Leetcode 215. Kth Largest Element in an Array

Click here for the code.

import heapq

class Solution:
def findKthLargest(self, nums: List[int], k: int):
    
    # creating max-heap
    nums = [i*(-1) for i in nums]
    heapq.heapify(nums)
    
    for i in range(k):
        item = heapq.heappop(nums)

    return item*(-1)

----

1. Sort an almost sorted array
2. Merge K Sorted Arrays.

Python Implementation

Python has the heapq module which creates a min-heap. To create a max-heap, multiply the numbers with $(-1)$ and create a min-heap and while popping element, return poped_item*(-1)

Time Complexity:

heapq is a binary heap, with $O(\log n)$ push and $O(\log n)$ pop

The algorithm you show takes $O(n \log n)$ to push all the items onto the heap, and then $O((n-k) \log n)$ to find the kth largest element. So the complexity would be $O(n \log n)$. It also requires $O(n)$ extra space.

• SO

TODO:

• Implement Heap datastructure

Reference:

• TDS: heap data Structure
• G4G: Binary Heap

Quick Select

Leetcode: 221. Maximal Square

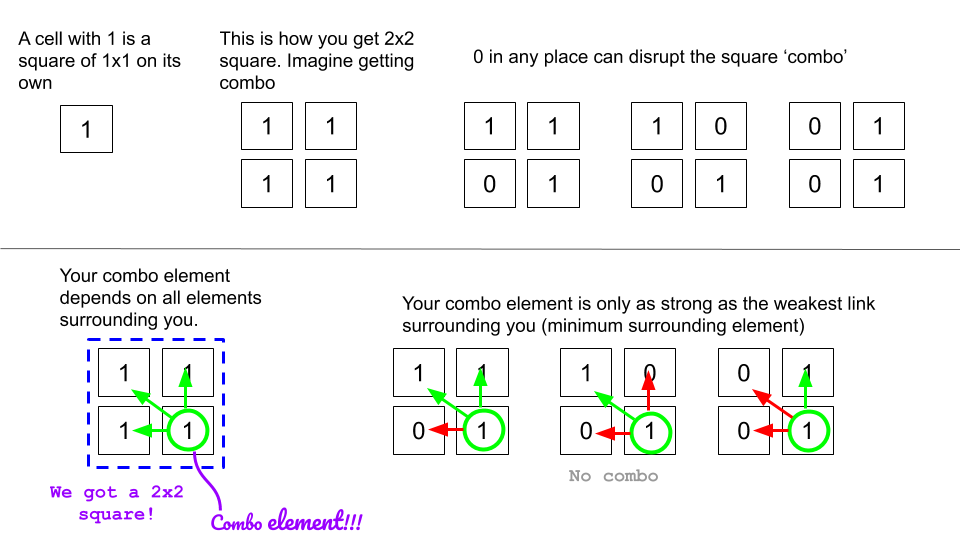
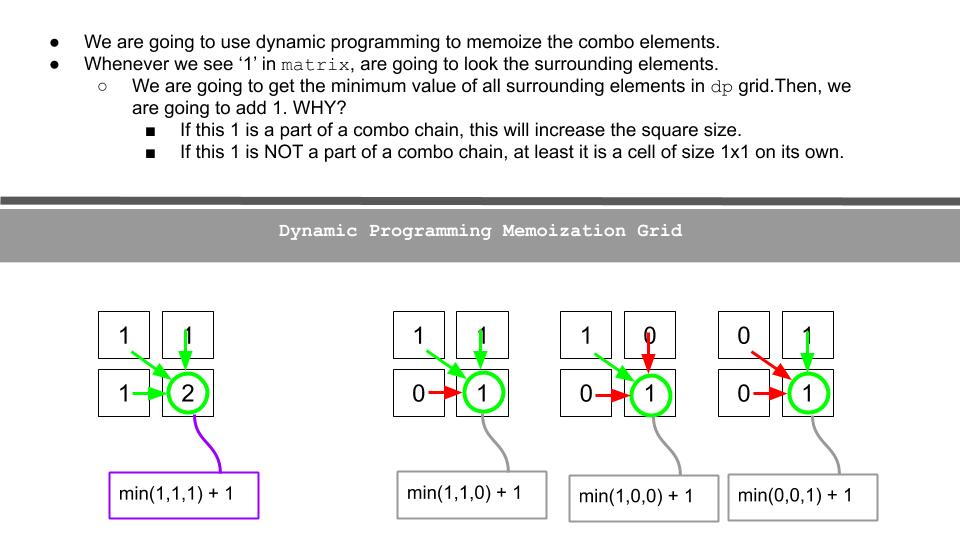
Here we are drawing squares from top left corner to bottom right corner. Therefore, by “surrounding elements”, we mean cells above the corner cell and the cells on the left of the corner cell.

Building DP grid to memoize

• We are going to create a dp grid with initial values of $0$.
• We are going to update dp as described in the following figure.

Bigger Example

Let’s try to see a bigger example. We go over one cell at a time row by row in the matrix and then update our dp grid accordingly. Update max_side with the maximum dp cell value as you update.

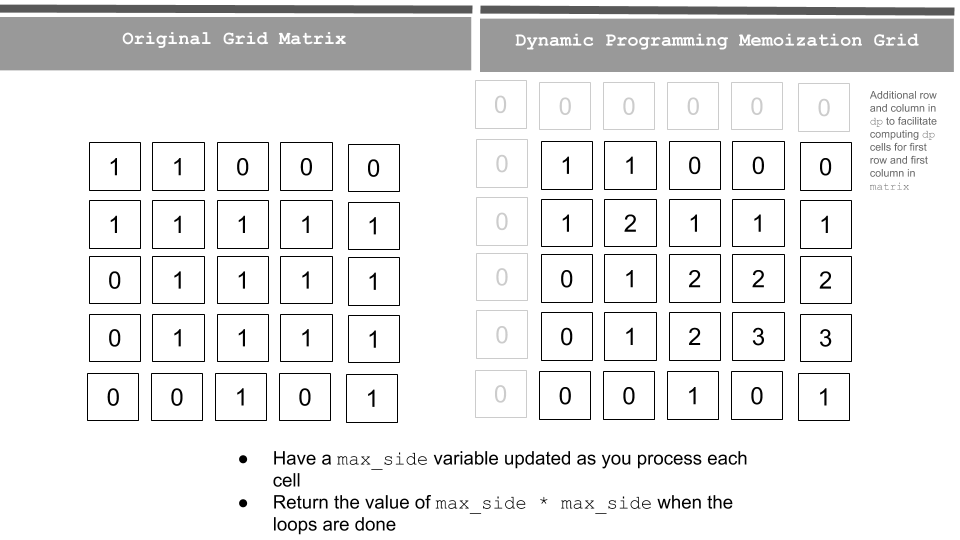
Reference:

• Explanation
• Youtube Video

Difference between bounded and unbounded 0/1 knapsack

In Recursive Approach

The only difference between the 0/1 Knapsack bounded and unbounded problem is that, after including the item

• unbounded: We recursively call to process all the items (including the current item)
• currentIndex is not increased while calling the recursive function

profit1 = 0
if weights[currentIndex] <= capacity:
    profit1 = profits[currentIndex] + solve_knapsack_recursive(
      profits, weights, capacity - weights[currentIndex], currentIndex)

• bounded: We recursively call to process all the remaining items (excluding the current item)
  • currentIndex+1 is introduced while calling the recursive function

profit1 = 0
if weights[currentIndex] <= capacity:
    profit1 = profits[currentIndex] + solve_knapsack_recursive(
      profits, weights, capacity - weights[currentIndex], currentIndex+1)

In Bottom-Up Approach

0/1 Bounded: for each item at index i ($0 \leq i \lt items.length$) and capacity c ($0 \leq c \leq capacity$), we have two options:

1. Exclude the item at index i. In this case, we will take whatever profit we get from the sub-array excluding this item => profit_exclude = dp[i-1][c]
2. Include the item at index i if its weight is not more than the capacity. In this case, we include its profit profit_include = profit[i] + dp[i-1][c-weight[i]]
   • plus the state c-weight[i] for rest of the item (excluding)
3. dp[index][c] = max(profit_include, profit_exclude)

Un-Bounded: for each item at index i ($0 \leq i \lt items.length$) and capacity c ($0 \leq c \leq capacity$), we have two options:

1. Exclude the item at index i. In this case, we will take whatever profit we get from the sub-array excluding this item => profit_exclude = dp[i-1][c]
2. Include the item at index i if its weight is not more than the capacity. In this case, we include its profit profit_include = profit[i] + dp[i][c-weight[i]]
   • plus the state c-weight[i] for the item (including)
3. dp[index][c] = max(profit_include, profit_exclude)

for both the approach, the subtle difference is at step 2, after adding the profit.

• Bounded: dp[i-1][c-weight[i]]
• Unbounded: dp[i][c-weight[i]]

Rest same.

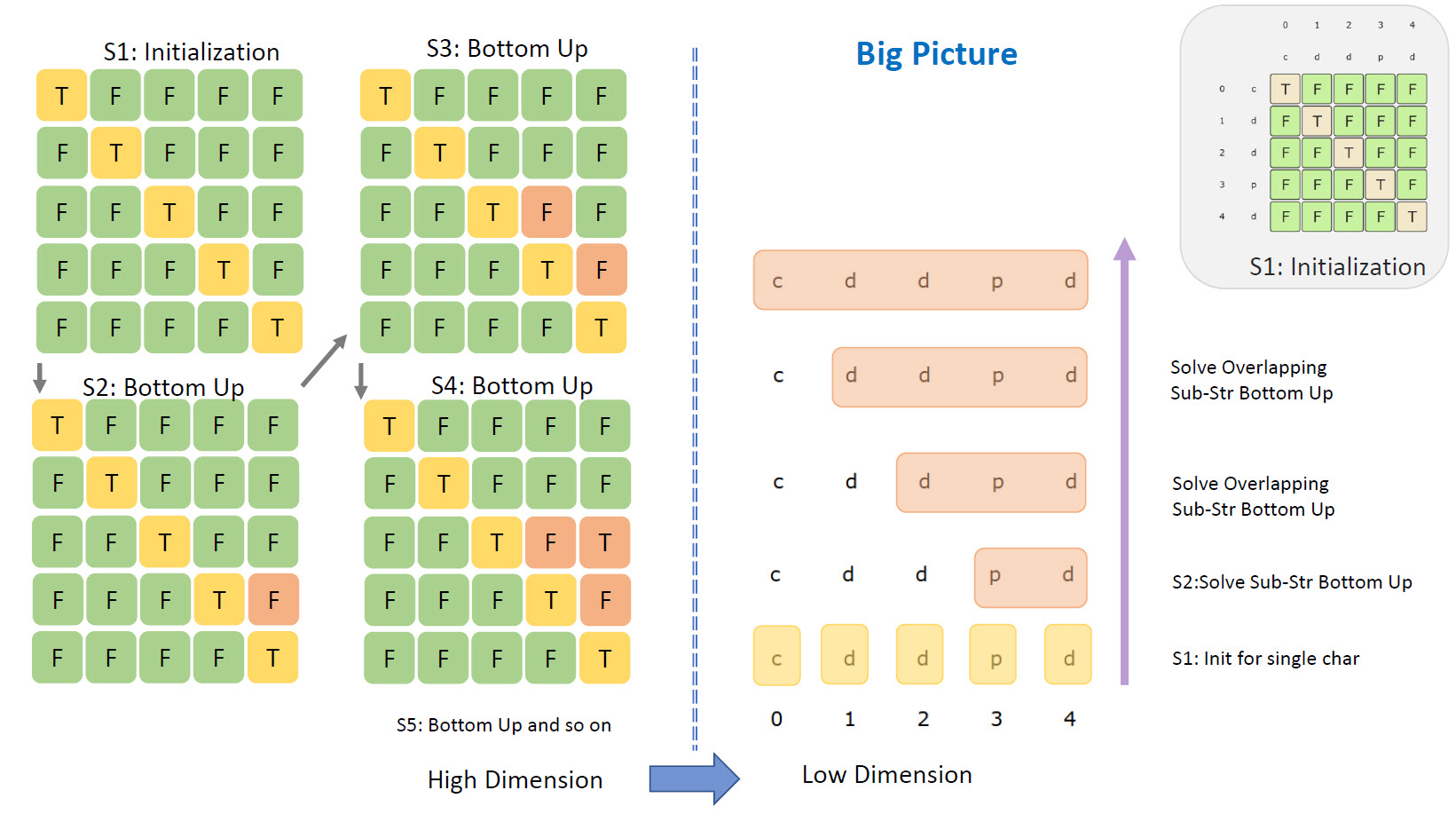
How to Visualize DP Bototm Up for Longest Palindromic Substring or Subsequence

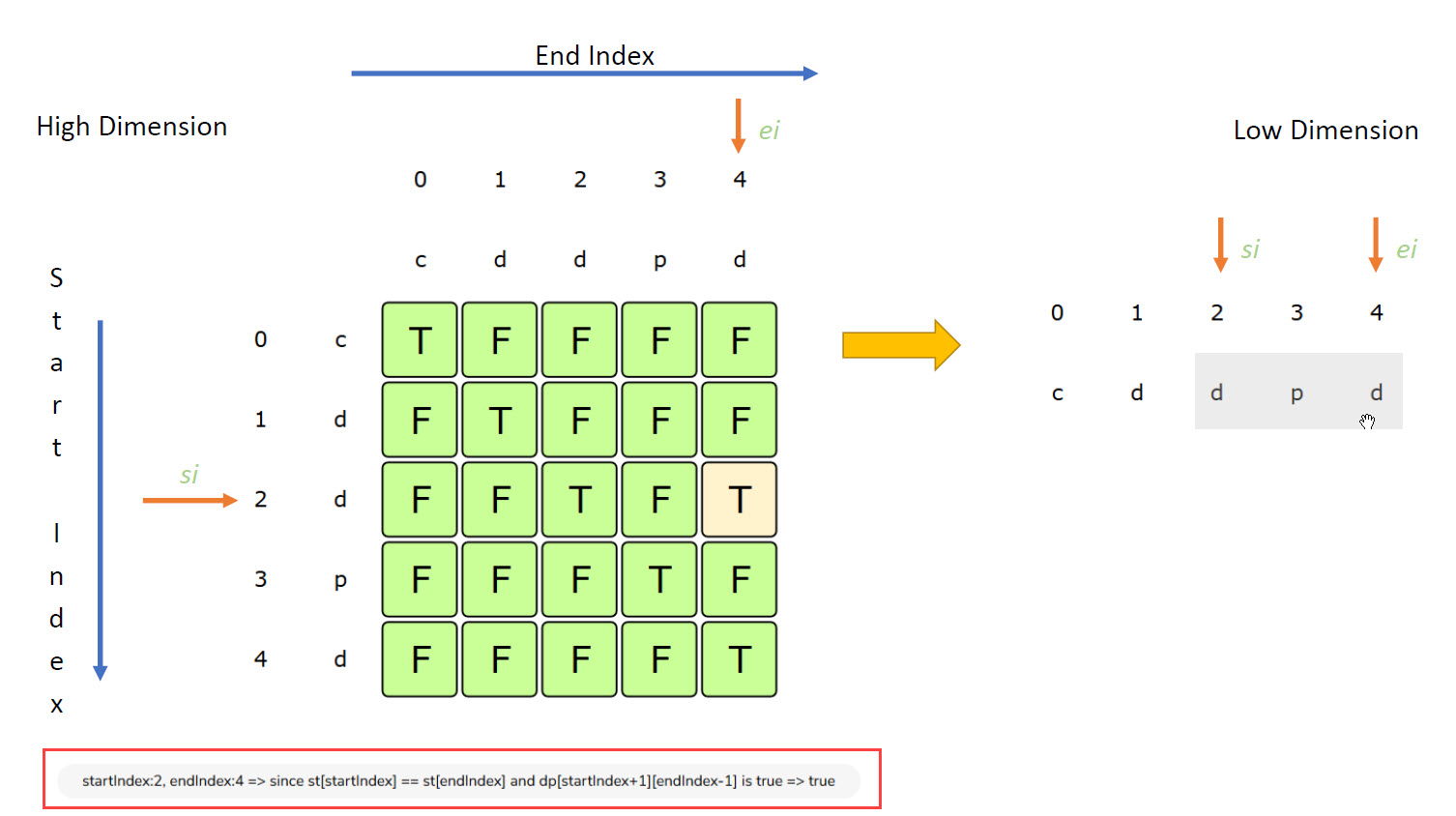
The below example is to find Longest Palindromic Substring for string cddpd

• si = 2 and ei = 4: means we are checking substring dpd.
• Now st[si] == st[ei] as both are d
• So check if (si+1:ei-1) is sub string or not ?
• si+1 = 3, ei-1 = 3 i.e from st[3:3], which is the char p and from the dp[][] we see dp[3][3] = T , so overall dp[2][4] = T

This is the overall thought processing, how the 2 things are related in High Dimension i.e DP 2D matrix with Low Dimension i.e 1D string.

Difference between Longest Palindromic Substring and Longest Palindromic Subsequence

A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements.

A substring is a continuous sequence.

Longest Palindromic Subsequence

Example 1:

Input: "abdbca"
Output: 5
Explanation: LPS is "abdba".

Example 2:

Input: = "cddpd"
Output: 3
Explanation: LPS is "ddd".

The abdba from example 1, is not continuous (not a substring) as the problem was to find Longest Palindromic Subsequence. So while implementing, then it’s NOT NECESSARY, if str[start] == str[end] then remaining elements in between str[strat+1:end-1] is also a palindrome.

if st[endIndex] == st[startIndex]: 
  dp[startIndex][endIndex] = 2 + dp[startIndex + 1][endIndex - 1]
else: 
  dp[startIndex][endIndex] = Math.max(dp[startIndex + 1][endIndex], dp[startIndex][endIndex - 1])

Longest Palindromic Substring

Example 1:

Input: "abdbca"
Output: 3
Explanation: LPS is "bdb".

Example 2:

Input: = "cddpd"
Output: 3
Explanation: LPS is "dpd".

if st[startIndex] == st[endIndex]:
    remaining_length = endIndex - startIndex - 2
    if remaining_length <=1 or dp[startIndex+1][endIndex-1] == True:
        dp[startIndex][endIndex] = True

• Here the problem is to find Longest Palindromic Substring, then it’s NECESSARY if str[start] == str[end] then remaining elements in between str[strat+1:end-1] is a palindrome.

• dp[startIndex+1][endIndex-1] == True denotes if remaining in between elements are also palindrome.

Spiral Matrix

Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.

Input:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]
Output: [1,2,3,6,9,8,7,4,5]

Solution Explanation:

If the video is not opening, click here

Search in Rotated Sorted Array

If the video is not opening, click here

Comprehensive Data Structure and Algorithm Study Guide

• Leetcode: Gold Mine

Leetcode 210: Course Schedule

• Problem Statement

Problem Statement

There are a total of n courses you have to take labelled from 0 to n - 1.

Some courses may have prerequisites, for example, if prerequisites[i] = [ai, bi] this means you must take the course bi before the course ai.

Given the total number of courses numCourses and a list of the prerequisite pairs, return the ordering of courses you should take to finish all courses.

If there are many valid answers, return any of them. If it is impossible to finish all courses, return an empty array.

Solution:

This is the classical problem about topological sort: (for more details you can look here. The basic idea of topological order for directed graphs is to check if there cycle in this graph.

For example if you have in your schedule dependencies like 0 -> 5, 5-> 3 and 3 -> 0, then we say, that cycle exists and in this case we need to return False.

Important: There are different ways to do topological sort, We use dfs. The idea is to use classical dfs traversal, but color our nodes into 3 different colors,

• 0 (white) for node which is not visited yet
• 1 (gray) for node which is in process of visiting (not all its neibours are processed)
• 2 (black) for node which is fully visited (all its neibours are already processed).

from collections import defaultdict
class Solution:
    def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
        
        self.NOT_VISITED = 0
        self.IN_PROCESS = 1 # in the process of visiting neighbours
        self.VISITED = 2 # when all neighbours are visited
        
        self.graph = defaultdict(list)
        
        for course in prerequisites:
            dest, src = course[0], course[1]
            self.graph[src].append(dest)
            
        self.visited_list = {node: self.NOT_VISITED for node in range(numCourses)}
        
        self.order = []
        self.has_cycle = 0
        
        for node in range(numCourses):
            if self.visited_list[node] == self.NOT_VISITED:
                self.dfs(node)
        
        # return in reverse order as in the given input in Leetcode the
        # src, dest were in reverse order
        return [] if self.has_cycle == 1 else self.order[::-1]
        
    def dfs(self, node: int):
        
        if self.has_cycle == 1: return
        
        # begin of recursion
        self.visited_list[node] = self.IN_PROCESS
        
        if node in self.graph:
            for neib in self.graph[node]:
                if self.visited_list[neib] == self.NOT_VISITED:
                    self.dfs(neib)
                elif self.visited_list[neib] == self.IN_PROCESS:
                    self.has_cycle = 1
        
        # end of recursion
        self.visited_list[node] = self.VISITED
        self.order.append(node)

Note: Uderstanding the classical DFS is very beneficial for many graph related question.

Kadane Algorithm

Write an efficient program to find the sum of contiguous subarray within a one-dimensional array of numbers which has the largest sum.

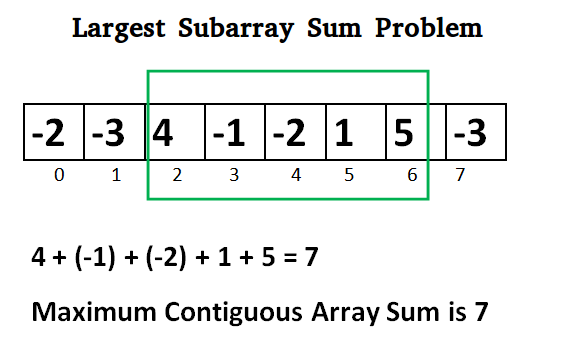
Explanation: Simple idea of the Kadane’s algorithm is to look for all positive contiguous segments of the array (max_ending_here is used for this).

• Keep track of maximum sum contiguous segment among all positive segments (max_so_far is used for this).
• Each time we get a positive sum compare it with max_so_far and update max_so_far if it is greater than max_so_far

def maxSubArraySum(a,size): 
       
    max_so_far = 0
    max_ending_here = 0
       
    for i in range(0, size): 
        max_ending_here = max_ending_here + a[i] 

        # if max_ending_here < 0, reset to 0
        max_ending_here = max(0, max_ending_here)
        max_so_far = max(max_so_far, max_ending_here)
        
    return max_so_far 

# Driver function to check the above function  
a = [-13, -3, -25, -20, -3, -16, -23, -12, -5, -22, -15, -4, -7] 
print "Maximum contiguous sum is", maxSubArraySum(a,len(a)) 

# Maximum contiguous sum is 7

Similar question:

• LC152: Maximum Product Subarray [Try yourself]

Why this problem is important?

Many time the question will not give the array $a$ directly. Rather, the question will be twisted such that, the input array is $a’$.

You need to convert array $a’$ to $a$ and map the problem to Kadane’s algo.

See the next problem.

Reference:

• geeks4geeks

Best Time to Buy and Sell Stock

Say you have an array for which the ith element is the price of a given stock on day i.

If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.

Note that you cannot sell a stock before you buy one.

Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
             Not 7-1 = 6, as selling price needs to be larger than buying price.

Say the given array is:

[7, 1, 5, 3, 6, 4]

If we plot the numbers of the given array on a graph, we get:

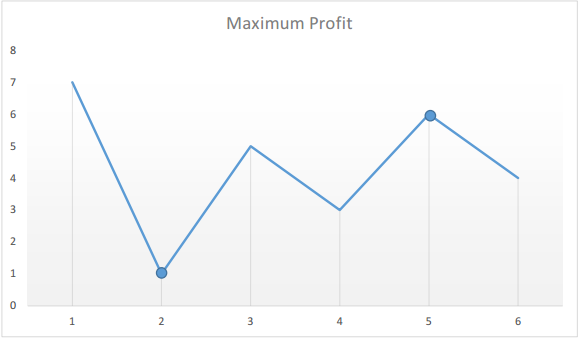
The points of interest are the peaks and valleys in the given graph. We need to find the largest peak following the smallest valley.

Now this problem can be mapped to Kadane’s algo.

Solution:

The logic to solve this problem is same as “max subarray problem” using Kadane’s Algorithm.

For the given input $a’ = {1, 7, 4, 11}$, convert it to daily profit array $a ={0, 6, -3, 7}$ and then your task is to find the max sum contiguous subarray $\rightarrow$ Kadane’s algo

def maxProfit(prices: List[int]) -> int:

    n = len(prices)
    if n < 2: return 0
    
    profit = [0]*n
    for i in range(1,n):
        profit[i] = prices[i] - prices[i-1]
    
    print(profit)
    max_profit_ending_here = 0
    max_profit_so_far = 0
    
    for i in range(1,n):
        max_profit_ending_here += profit[i]
        max_profit_ending_here = max(0, max_profit_ending_here)
        max_profit_so_far = max(max_profit_so_far, max_profit_ending_here)
        
        
    return max_profit_so_far

LC79. Word Search

Given a 2D board and a word, find if the word exists in the grid.

The word can be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once.

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

Given word = "ABCCED", return true.
Given word = "SEE", return true.
Given word = "ABCB", return false.

• Youtube

Construct binary tree from tree traversal

In general you need to:

DO

• Find the root of the tree. [obtain from preorder or postorder list]
  • Find the index of root.val , say idx, in the inorder list
• Subset of nodes which will be in the left subtree [inorder[:idx]]
• Subuset of nodes in the right subtree [inorder[idx+1:]]

RECUR

finding root in preorder or postorder is slightly different

from inorder and postorder traversal

Base implementation

class Solution:
    def buildTree(self, inorder, postorder):
        if not inorder or not postorder:
            return None
        
        root = TreeNode(postorder.pop())
        inorderIndex = inorder.index(root.val) # Line A

        root.right = self.buildTree(inorder[inorderIndex+1:], postorder) # Line B
        root.left = self.buildTree(inorder[:inorderIndex], postorder) # Line C

        return root

The code is clean and short. However, if you give this implementation during an interview, there is a good chance you will be asked, “can you improve/optimize your solution?”

Why? Take a look at Line A, Line B and Line C. Line A takes $O(N)$ time. Line B and C takes $O(N)$ time and extra space. Thus, the overall running time and extra space is $O(N^2)$.

Running time $O(N^2)$: Because here for each call to line B and line C, searching time at line A is $O(N)$. So it’s taking $O(N^2)$.

So this implementation has a very bad performance, and you can avoid it.

optimized implementation use dict() to search in $O(1)$

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        
        self.key_map = {v:i for i,v in enumerate(inorder)}
        self.postorder = postorder
        return self.helper(0, len(inorder)-1)
        
    def helper(self, left:int, right:int):
        
        if left > right: return None
        root = TreeNode(self.postorder.pop())
        idx = self.key_map[root.val]
        root.right = self.helper(idx+1, right) # pay attention
        root.left = self.helper(left, idx-1) # pay attention
        return root

Note:

• root.right is called first before root.left as it’s using postorder traversal and we are scanning the postorder list from right side, which holds the right subtree elements at the right side.
• • The length (right - left) denotes the number of nodes in the respective subtree and also decides the number of time it should apply recursion in the respective branch.

Reference:

• Youtube

from inorder and preorder traversal

def buildTree(preorder: List[int], inorder: List[int]) -> TreeNode:
    
    if len(preorder) == 0:return None
    
    root = TreeNode(preorder[0])
    mid_idx =  inorder.index(root.val)
    root.left = buildTree(preorder[1:mid_idx+1], inorder[:mid_idx])
    root.right = buildTree(preorder[mid_idx+1:], inorder[mid_idx+1:])
    return root

With same logic, here is the optimizied version

class Solution(object):
    def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: TreeNode
        """
        
        inor_dict = {}
        for i, num in enumerate(inorder):
            inor_dict[num] = i
        pre_iter = iter(preorder)
        
        def helper(start, end):
            if start > end:return None
            root_val = next(pre_iter)
            root = TreeNode(root_val)
            idx = inor_dict[root_val]
            root.left = helper(start, idx-1) # pay attention
            root.right = helper(idx+1, end) # pay attention
            return root
        
        return helper(0, len(inorder) - 1)

Note:

• root.left is called first before root.right as it’s using preorder traversal and we are scanning the preorder list from left side, which holds the left subtree elements at the left side.
• The length (end - start) denotes the number of nodes in the respective subtree and also decides the number of time it should apply recursion in the respective branch.

Reference:

• Youtube

Interesting problems:

• Find peak in 1D and 2D surface MIT

Backtracking patterns and variations

Find Permutation

Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.

Example:

# Input: nums = [1,2,3]
# Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

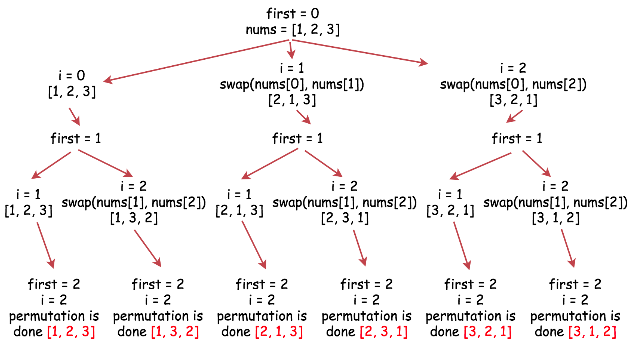
*in the below solution first == cur_pos

*image courtsey leetcode

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        
        self.n = len(nums)
        self.res = []
        self.traverse(nums, 0)
        return self.res
        
        
    def traverse(self, nums, cur_pos):
        
        if cur_pos == self.n:
            # print(nums)
            self.res.append(nums[:])
        
        # iterate along the same level
        for i in range(cur_pos, self.n):
            
            # DO OPERATION
            nums[cur_pos], nums[i] = nums[i], nums[cur_pos]
            
            # go to the next level
            self.traverse(nums, cur_pos+1)
            
            # backtrack
            # UNDO OPERATION
            nums[cur_pos], nums[i] = nums[i], nums[cur_pos]

Combination sum

Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.

• The same number may be chosen from candidates an unlimited number of times.
• Two combinations are unique if the frequency of at least one of the chosen numbers is different.

Examples:

# Input: candidates = [2,3,5], target = 8
# Output: [[2,2,2,2],[2,3,3],[3,5]]

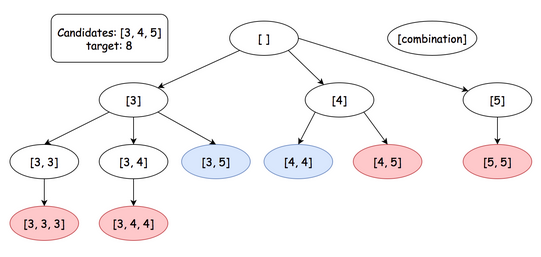
*image courtsey leetcode

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:

        self.results = []
        self.candidates = candidates
        self.traverse(target, [], 0)

        return self.results
        
    def traverse(self, remain, comb, start):
        if remain == 0:
            # make a deep copy of the current combination
            self.results.append(comb[:])
            return
        
        elif remain < 0:
            # Exceed the scope, stop exploration.
            return

        # Iterate along the same level
        for i in range(start, len(self.candidates)):
            
            # DO OPERATION -> add the number into the combination
            comb.append(self.candidates[i])
            
            # Go to the next level
            # Give the current number another chance, rather than moving on
            self.traverse(remain - self.candidates[i], comb, i)
            
            # Backtrack, 
            # UNDO operation -> remove the number from the combination
            comb.pop()

General Strategy:

Look carefully at the traverse() function and the comments. It’s basically traversing an n-arrary tree along level.

• for loop to traverse along the same level (travel horizontally)
  • DO operation (e.g: swap (e.g: permutation) or append (e.g: combination sum) etc as per the problem statement)
  • At current level recur i.e call traverse() (traverse vertically)
  • UNDO the same operation $\leftarrow$ BACKTRACK i.e go back to the previous tree level and find a new path.

Note:

Once one figures out how it works with the backtracking algorithm for this problem, one can go ahead and apply this hammer to solve a series of similar problems in leetcode.

• Subsets
• Subsets II
• Permutations
• Permutations II
• Combinations
• Combination Sum II
• Combination Sum III
• Palindrome Partition

Exercise:

1. DP: bellman-equations-reinforcement-learning