Domain Knowledge: Insurance

Content

  1. Content
  2. What is Exposure?
  3. What is TotalLoss?
    1. What is Constructive Total Loss:
  4. What is Partial Loss:
  5. What is Hull Loss:
  6. What is Liability?
  7. What is Liability Insurance?
  8. What Is Loss Development?
  9. What is Mortality Rate?
  10. What Is the Frequency-Severity Method?
    1. Frequency-Severity Method Explained
  11. What is Frequency-Severity Model?
  12. How to calculate the frequency model?
    1. Poisson Regression
    2. Why this is an advantage over the typical Linear Regression?
    3. Fitting a Poisson regression model
    4. Nonlinear Regression Structure
    5. Zero-Inflated Count Model
    6. Logistic Regression
      1. Logit and logistic functions
      2. Fit and interpretation
  13. What is Loss Ratio?
  14. What is Burning Cost?
  15. What is a Ceding Company?
  16. Exercise:

What is Exposure?

Exposure refers to an individual’s susceptibility to various risks encountered in daily life. It denotes the individual’s potential for accidents and other losses. Insurance companies evaluate the level of risk an individual faces and use it to calculate insurance premiums. For instance, the more frequently a person drives a car, the higher that individual’s exposure to accidents and other similar problems will be. In some cases, insurance companies refer to their insured entities as exposures too. This is because the policyholders represent risks to the insurance company, since the insurer will need to pay the appropriate benefits to the policyholders if they file a claim.

The number of policies, which have been written, denote the exposure. Say the insurer does $1000$ motor accident policies and $10$ wild-fire policies. Now the Insurer is exposed to motor accidents more than the wild-fire accidents. Because whenever any accident will happen, the insured will claim for money and insurer will lose money. So by doing more motor policies insurer is exposed to more motor risks. So number of policies for a category (motor accident) indicates the exposure to the risk of losing money due to accident of that category (motor accident).

Content

What is TotalLoss?

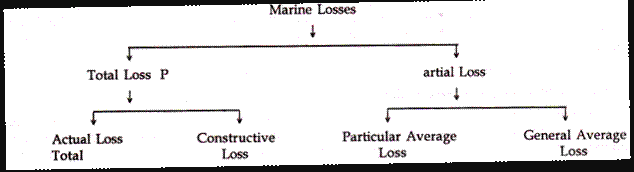
image

In insurance claims, a total loss or write-off is a situation where the lost value, repair cost or salvage cost of a damaged property, exceeds its insured value (the value which the insurer agreed to pay in the contract). Such a loss may be an actual total loss or a constructive total loss. Constructive total loss considers further incidental expenses beyond repair.

In a total loss, the insurer must indemnify (provide security) the assured in full, and ownership of the insured item thereby passes to the insurer under the legal process of subrogation (the substitution of one person or group by another in respect of a debt or insurance claim). Although the policy determines the level at which the loss becomes total rather than partial, nevertheless the assured (and NOT the insurer) has the final say as to whether he wishes to make a partial or total claim.

Actual total loss occurs under these following situations:

  • The subject-matter is completely destroyed.
  • The goods are so damaged that they cease to be a thing of the kind which were insured.
  • The insured is deprived of the subject-matter.

Example: When a ship is sunk or is completely destroyed by fire, it will be a case of actual total loss. There may be a case when the goods are so damaged that they do not look like goods which were insured e.g. if crockery is reduced to pieces, it is a case of actual total loss.

In another case if the insured is not able to get the things back i.e., if the ship is missing and there is no trace of it, it is also a case of actual total loss. In case of actual total loss the insured is entitled to recover full amount of loss. When the insured has been compensated, the title of goods passes on to the insurer. If some amount is received from the sale of damaged goods, the amount will go to the insurer and not to the insured.

Reference:

Content

What is Constructive Total Loss:

This occurs when the ship is abandoned for certain reasons. It is not commercially viable to retrieve the ship or cargo. The ship or the cargo is not wholly destroyed but it is not practicable to get it repaired and restore it to its original position. When a ship is badly damaged, and the cost of repairs is expected to be more than the value of the ship, it will be advisable to abandon the ship.

In the same way if the cargo is safe in the abandoned ship but the cost of bringing the cargo to the coast is more than the cost of cargo, then it will be proper to leave the cargo. In the case of constructive total loss, the insured gives a notice of abandonment and surrenders its interest in the subject-matter to the insurer. The insured can claim damage for total loss.

Reference:

Content

What is Partial Loss:

When the subject-matter is partially damaged, it will be a case of partial loss. It is of two types:

  1. Particular Average Loss:

A particular average loss has been defined as, a partial loss of subject-matter insured, caused by a peril insured against, and which is not general average loss. A particular average loss is not caused voluntarily. The insured subject-matter should be damaged and this damage should be caused by marine peril which is insured.

  1. General Average Loss:

A general average loss is caused voluntarily to avoid an impending danger. “A general average loss is one which is caused by an extra-ordinary sacrifice or expenditure voluntarily and reasonably made or incurred under fortuitous circumstances, for the sole purpose of preserving the common interest from an impending peril.”

If a ship is sinking because of overload, some of the cargo may be thrown out of the ship with a purpose to save the ship and the crew. It will be a case of general average loss.

Reference:

Content

What is Hull Loss:

Hull: The main body of a ship or other vessel, including the bottom, sides, and deck but not the masts, superstructure, rigging, engines, and other fittings.

  • A hull loss is an aviation accident that damages the aircraft beyond economical repair, resulting in a total loss.
  • The term also applies to situations in which the aircraft are missing, the search for their wreckage is terminated or when the wreckage is completely inaccessible.

Constructive hull loss factors other incidental expenses beyond repair, such as salvage, logistical costs of repairing the non-airworthy aircraft within the confines of the incident site, recertifying the aircraft, etc. Insurance policies covering any asset that is subject to depreciation, typically pay the insured a fraction of the cost of replacing the property, so that a loss may be deemed to be total although some residual value remains.

Reference:

Content

What is Liability?

When a person or organization is responsible for something, especially in law, that’s liability.

Liability insurance can cover you for

  • Legal costs
  • Compensation costs

that you might have to pay if you are proved to be the cause of harm to another person or business.

Does not mean your ability to lie about, though that could lead to liability.

What is Liability Insurance?

Liability insurance protects you against financial loss if your actions, your negligence or the condition of your property is found to cause a person to be injured or killed, or a person’s property to be damaged or destroyed or they suffer loss as a result of relying on your services or advice.

Liability insurance (also called third-party insurance) is a part of the general insurance system of risk financing to protect the purchaser (the “insured”) from the risks of liabilities imposed by lawsuits and similar claims and protects the insured if the purchaser is sued for claims that come within the coverage of the insurance policy.

Originally, individual companies that faced a common peril formed a group and created a self-help fund out of which to pay compensation should any member incur loss (in other words, a mutual insurance arrangement). The modern system relies on dedicated carriers, usually for-profit, to offer protection against specified perils in consideration of a premium.

Liability insurance is designed to offer specific protection against third-party insurance claims, i.e., payment is not typically made to the insured, but rather to someone suffering loss who is not a party to the insurance contract. In general, damage caused intentionally as well as contractual liability are not covered under liability insurance policies. When a claim is made,[1] the insurance carrier has the duty (and right) to defend the insured.

Liability products are most commonly taken out by businesses for risks involved in their day-to-day operation, but they are also built into many property insurance policies, for example liability cover in home and contents insurance.

Liability insurance covers two key financial risks. One is the legal cost of defending a claim. The second is the compensation that you may be directed to pay the injured or wronged party, plus their legal costs, if a claim against you is upheld.

These usually include an excess to be paid by the policyholder in the event of a claim, and generally set a limit on the total amount payable under the policy, as well as a per-claim limit.

Reference:

Content

What Is Loss Development?

Loss development is the difference between the final losses recorded by an insurer and what the insurer originally recorded.

Loss development seeks to account for the fact that some insurance claims take a long time to settle, and that estimates of the total loss that an insurer will experience will adjust as claims are finalized.

Reference

Content

What is Mortality Rate?

Mortality rate, or death rate, is a measure of the number of deaths (in general, or due to a specific cause) in a particular population, scaled to the size of that population, per unit of time. Mortality rate is typically expressed in units of deaths per $1,000$ individuals per year; thus, a mortality rate of $9.5$ (out of $1,000$) in a population of $1,000$ would mean $9.5$ deaths per year in that entire population, or $0.95$% out of the total. It is distinct from morbidity, which is either the prevalence or incidence of a disease, and also from the incidence rate (the number of newly appearing cases of the disease per unit of time).

In the generic form, mortality rates are calculated as:

$\frac{d}{p} * 10^n$

where $d$ represents the deaths occurring within a given time period, $p$ represents the size of the population in which the deaths occur and $10^n$ is a conversion factor from fraction to some other unit (such as multiplying by $10^3$ to get mortality rate per 1,000 individuals).

Reference:

Content

What Is the Frequency-Severity Method?

Frequency-severity method is an actuarial method for determining the

  • Frequency: Expected number of claims that an insurer will receive during a given time period
  • Severity: How much the average claim will cost.

Frequency-severity method uses historical data to estimate the average number of claims and the average cost of each claim.

The method multiplies the average number of claims by the average cost of a claim.

NOTE: Frequency model can be thought of as Logistic Regression problem where you want to know if an accident will happen or not? i.e. instead of how many accidents this aircraft can face (linear regression), you are answering whether this aircraft will face any accident or not (logistic regression).

It’s a success of failure model, which can be modelled with GLM with binomial (binary output) family of functions.

Frequency-Severity Method Explained

In the frequency-severity method, frequency refers to the number of claims that an insurer anticipates will occur over a given period of time. But the claim will only happen if there is an accident. So frequency model can be reformulate to if there will be an accident for an aircraft. A probabilistic method is helpful to identify the strengths of chances.

If the frequency (probability) is high, it means that a large number of claims is expected to occur.

Severity refers to the cost of a claim. A high-severity claim is more expensive than an average claim, and a low-severity claim is less expensive than the average claim. Average costs of claims are estimated based on historical data.

For instance, consider a prospective home buyer considering the purchase of a beach house in Miami. This part of the Florida coast averages one hurricane per year. With the potential for complete destruction so high and so frequent, the frequency-severity method would indicate that an insurance company should avoid underwriting a policy for this beach house.

Reference:

Content

What is Frequency-Severity Model?

This browser does not support PDFs. Please download the PDF to view it: Download PDF.

</embed>

Reference:

Content

How to calculate the frequency model?

Difference between Machine Learning approach and Statistical approach is that the former doesn’t assume anything about the distribution of the data while the later does.

Example: Say we have a dataset of number of hurricanes happen in US for different year. This dataset contains lots of counts.

##   Year All MUS G FL E
## 1 1851   1   1 0  1 0
## 2 1852   3   1 1  2 0
## 3 1853   0   0 0  0 0
## 4 1854   2   1 1  0 1
## 5 1855   1   1 1  0 0
## 6 1856   2   1 1  1 0

Now in typical ML approach it will go for any regression based approach with regularization to avoid overfitting. A good starting point will be Random Forest Regressor. Good part is you don’t assume any distribution of the data. But here you will have a point estimate.

Butt traditional Statistical Learning will assume the data distribution based on the problem statement. Like for this kind of problem with count data, it has been seen the response variable follows poisson distribution. So they will try to fit a GLM with distribution family poisson. This also helps them to learn the mean and variance of the distribution instead of just the point estimate. This is one of the big difference between this 2 approaches.

This statistical approach also helps to answer the following questions:

## Q. The probability of five hurricanes?
## Q. The probability of two hurricanes?
## Q. What is the probability of more than two hurricanes?
  • The parameter of interest is the annual rate. Given the rate, you have a probability distribution for any possible hurricane count.

Poisson Regression

  • The model of choice for count data is Poisson regression.
  • Poisson regression assumes the response variable has a Poisson distribution and the logarithm of the expected value of the response variable is modeled with a linear combination of explanatory variables (log-linear model).

Why this is an advantage over the typical Linear Regression?

Say if we use typical linear regression, then the predicted count may come as negative (see example in the given link), which is completely false. But with the assumption of poison distribution, you will never that kind of situation.

# linear regression
lrm = lm(All ~ SOI + NAO + SST + SSN, data = df)
predict(lrm, newdata = data.frame(SOI = -3, NAO = 3, SST = 0, SSN = 250))
##       1 
## -0.3181

The prediction results in a negative number that is not a count. It indicates the climate conditions are unfavorable for hurricanes, which is true but the number has no physical meaning. This is a problem.

A Poisson regression model that specifies the logarithm of the annual hurricane rate is an alternative. The assumption is that the hurricanes are independent in the sense that the arrival of one hurricane will not make another one more or less likely, but the rate of hurricanes varies from year to year due to the covariates.

The Poisson regression model is expressed as

$ \log(\lambda) = \beta_0+\beta_1 x_1 + \ldots +\beta_p x_p $

Here there are $p$ covariates (indicated by the $x_i$’s) and $p+1$ parameters ($\beta_i$’s).

NOTE:

  • The model uses the logarithm of the rate as the response variable, but it is linear in the regression structure.
  • It is not the same as a linear regression on the logarithm of counts.
  • The model coefficients are determined by the method of maximum likelihood.

Fitting a Poisson regression model

  • The method of maximum likelihood is employed in the glm() function to determine the model coefficients.
  • The Poisson regression model is a type of generalized linear model (GLM) in which the logarithm of the rate of occurrence is a linear function of the covariates (predictors).

To fit a Poisson regression model to U.S. hurricanes and save the model as an object, type

prm = glm(All ~ SOI + NAO + SST + SSN, data = df, family = "poisson")

Nonlinear Regression Structure

Poisson regression specifies a linear relationship between your covariates and the logarithm of the hurricane rate. Linearity in the regression structure can be restrictive if the influence of a covariate changes over its range. Multivariate adaptive regression splines (MARS) is a form of regression introduced by Friedman (1991) that allows for such nonlinearities.

MARS builds models of the form

$ \hat f(x) = \sum_{i=1}^k c_i B_i(x) $

where $B_i(x)$ is a basis function and $c_i$ is a constant coefficient. The model is thus a weighted sum of the $k$ basis functions.

The earth() function in the earth package (Milborrow 2011) provides functionality for MARS. The syntax is similar to other models in R. Here you create a model using MARS for your hurricane counts and the same environmental covariates by typing

require(earth)
mars = earth(All ~ SOI + NAO + SST + SSN, data = df, glm = list(family = "poisson"))

Zero-Inflated Count Model

The Poisson regression model is a good place to start when working with count data but it might not be good enough when data exhibit over-dispersion or when there are a large number of zero values.

These kinds of data can be handled with zero-inflated models.

Zero-inflated count models combine a point mass at zero and a count distribution. The gives you two sources of zeros:

  1. From the point mass
  2. From the count distribution.

Usually

  • the count model is a Poisson regression
  • the point mass is a Binomial regression.

or example, to model your U.S. hurricane counts where the count model uses all four covariates and where the binomial model uses only the SST variable, type

require(pscl)
zim = zeroinfl(All ~ SOI + NAO + SST + SSN | SST, data = df)

The model syntax includes a vertical bar $( \vert )$ to separate the covariates between the two model components. The returned object is of class zeroinfl and is similar to the object of class glm.

Logistic Regression

We would like to have a model that predicts a hurricane’s group membership based on where the hurricane originated.

Logistic regression is the model of choice when your response variable is dichotomous i.e. has binary outputs.

The focus is to predict the occurrence of the event. Instead of what is the probability of occurrence of 2 hurricanes, if there will be an accident? Whose answer is yes or no.

Logistic regression is a generalization of the linear regression model (like Poisson regression) where the response variable does not have a normal distribution and the regression structure is linear in the covariates.

Like Poisson regression the model coefficients are determined using the method of maximum likelihood.

Logit and logistic functions

Linear regression is not the appropriate model for binary data. It violates the assumption of equal variance and normality of residuals resulting in invalid standard errors and erroneous hypothesis tests. In its place you use a generalized linear model as you did above with the count data.

However, instead of using the logarithm as the link between the response and the covariates as you did in the Poission regression model, here you use the logit function. The logit of a number $\pi$ between $0$ and $1$ is

$ {logit}(\pi)=\log\left( \frac{\pi}{1-\pi} \right) =\log(\pi)-\log(1-\pi) $

If $\pi$ is a probability then $\frac{\pi}{(1-\pi)}$ is the corresponding odds, and the logit of the probability is the logarithm of the odds.

  • Odds are expressed as for:against (read: for to against) something happening. So the odds of a hurricane strike that is posted at $1:4$ has a $20\%$ chance of occurring.

The logistic regression model is expressed statistically as

$ {logit}(\pi) = \beta_0 + \beta_1 x_1 + \ldots +\beta_p x_p = \beta_0 +\Sigma_{i=1}^p \beta_i x_i $

where $\pi$ is the mean. There are $p$ covariates (i.e. predictors) ($x_i$’s) and $p+1$ parameters ($\beta_i$’s).

  • Substitute the $logit(\pi)$ with $\frac{\pi}{1-\pi}$
  • Take $\exp()$ on both side and rearrange and you will get
$ \pi = \frac{\exp(\beta_0 +\Sigma_{i=1}^p \beta_i x_i)}{1+\exp(\beta_0 +\Sigma_{i=1}^p \beta_i x_i)} = \frac{\exp(\alpha)}{1+\exp(\alpha)} $

where $\alpha=\beta_0 +\Sigma_{i=1}^p \beta_i x_i = logit(\pi)$

To convert $logit(\pi)$ to $\pi$ (probability of occurrence) you use the logistic function (inverse of the logit function) given as

$ {logistic}(\alpha) = \frac{1}{1 + \exp(-\alpha)} = \frac{\exp(\alpha)}{1 + \exp(\alpha)} $

Fit and interpretation

To fit a logistic regression model to hurricane type with latitude as the covariate and saving the model as an object, type

lorm = glm(tb ~ FirstLat, data = bh, family = "binomial")

The syntax is similar to the Poisson regression model, but here the family is binomial. The formula is read hurricane type is modeled as a function of formation latitude.

for more details, read the bellow link thoroughly

Reference:

Content

What is Loss Ratio?

A loss ratio is a ratio of losses to gains, used normally in a financial context. It is the opposite of the gross profit ratio (commonly known as the gross profit margin).

For insurance, the loss ratio is the ratio of total losses incurred (paid and reserved) in claims plus adjustment expenses divided by the total premiums earned. For example, if an insurance company pays $60$ in claims for every $100$ in collected premiums, then its loss ratio is $60\%$ with a profit ratio/gross margin of 40% or $40$. Some portion of those $40$ dollars must pay all operating costs (things such as overhead and payroll), and what is left is the net profit.

Loss ratios for property and casualty insurance (e.g. motor car insurance) typically range from $40\%$ to $60\%$. Such companies are collecting premiums more than the amount paid in claims. Conversely, insurers that consistently experience high loss ratios may be in bad financial health. They may not be collecting enough premium to pay claims, expenses, and still make a reasonable profit.

Content

What is Burning Cost?

The burning cost is an experience-rating method most commonly used in nonproportional reinsurance when there is sufficient credible claims experience.

The burning cost adjusts the actual historical losses and translates them to the prospective reinsurance period. Strain defines the burning cost as, “The ratio of actual past reinsured losses to ceding company’s subject matter premium (written or earned) for the same period. Used to analyze past reinsurance experience or to project the future.”

The burning cost is most useful for lower layers where there is significant claims experience for the results to be meaningful and predictive. When there is no sufficient claims experience, alternative rating methods might be used, for example, the exposure rating method.

Basic formula:

$ \frac{LossPaid + Outstanding}{NetPremiumIncome}*Loading = Rate $

The calculation is adjusted each year until all losses have been settled. If the rate calculated fall below the minimum, the minimum rate applies. If the rate calculated exceeds the maximum, then maximum rate is applied.

Reference:

What is a Ceding Company?

A ceding company is an insurance company that passes the part or all of its risks from its insurance policy portfolio to a reinsurance firm. Passing off risk in this manner allows the ceding company to hedge against undesired exposure to loss and frees up capital to use in writing new insurance contracts.

Exercise:

  1. What is Survival Analysis?
  2. What is mortality?
  3. What is Loss Ratio and Burning cost?

Back to Top

Published on January 19, 2020