Content

1. Content
2. Introduction
3. Implementation
4. Theory
   1. Choice of $f(x_i)$ and $g(x_i)$
   2. Choice of Loss Function
   3. Link between PCA and Autoencoders
   4. Regularization in autoencoders
   5. Denoising Autoencoder

Introduction

According to this blog:

Autoencoder is an unsupervised artificial neural network that learns how to efficiently compress and encode data then learns how to reconstruct the data back from the reduced encoded representation to a representation that is as close to the original input as possible.

Autoencoder, by design, reduces data dimensions by learning how to ignore the noise in the data.

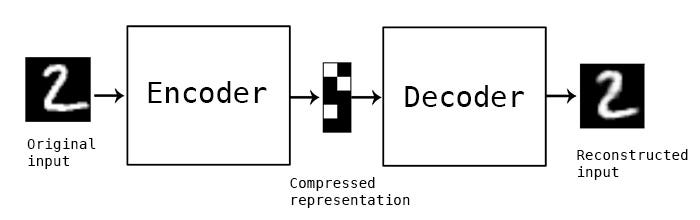
From architecture point of view, it looks like this:

Implementation

According to this wonderful notebook we can build the autoencoder as follows

##########################
### MODEL
##########################

class Autoencoder(torch.nn.Module):

    def __init__(self, num_features):
        super(Autoencoder, self).__init__()
        
        ### ENCODER
        self.linear_1 = torch.nn.Linear(num_features, num_hidden_1)
        # The following to lones are not necessary, 
        # but used here to demonstrate how to access the weights
        # and use a different weight initialization.
        # By default, PyTorch uses Xavier/Glorot initialization, which
        # should usually be preferred.
        self.linear_1.weight.detach().normal_(0.0, 0.1)
        self.linear_1.bias.detach().zero_()
        
        ### DECODER
        self.linear_2 = torch.nn.Linear(num_hidden_1, num_features)
        self.linear_1.weight.detach().normal_(0.0, 0.1)
        self.linear_1.bias.detach().zero_()
        

    def forward(self, x):
        
        ### ENCODER
        encoded = self.linear_1(x)
        encoded = F.leaky_relu(encoded)
        
        ### DECODER
        logits = self.linear_2(encoded)
        decoded = torch.sigmoid(logits)
        
        return decoded

    
torch.manual_seed(random_seed)
model = Autoencoder(num_features=num_features)
model = model.to(device)

optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

Theory

Listen to the lecture 7 by Prof. Mitesh

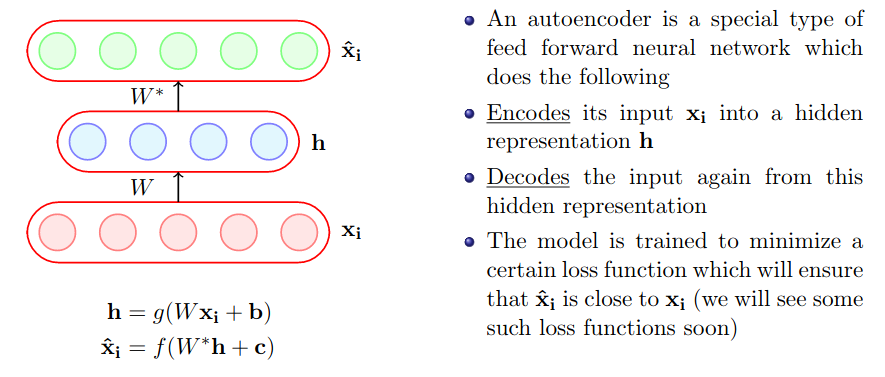
Choice of $f(x_i)$ and $g(x_i)$

Choice of Loss Function

for mathematical proof check slide 11-12 of Lecture 7 by Prof. Mitesh

for mathematical proof check slide 13-14 of Lecture 7 by Prof. Mitesh

Link between PCA and Autoencoders

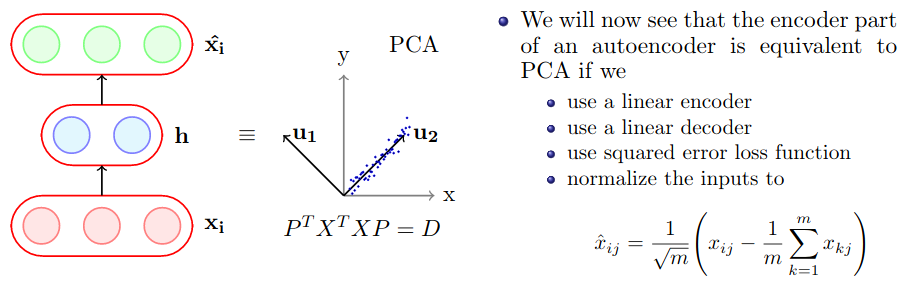
for mathematical proof check slide 17-21 of Lecture 7 by Prof. Mitesh

Regularization in autoencoders

• The simplest solution is to add a L2-regularization term to the objective function

• Another trick is to tie the weights of the encoder and decoder i.e. , $W^*=W^T$.
• This effectively reduces the capacity of Autoencoder and acts as a regularizer.

• Different regularization gives rise to different Autoencoder as seen in the above slide. The second and third regularization gives rise to Spare AE and Contractive AE. For more details check the slide.

Denoising Autoencoder

Reference:

• Very Important Lecture 7, both slide and video

Back to Top