Survey - Residual Network
Content
Introduction
He et. al in his seminal paper Deep Residual Learning for Image Recognition presented this idea of Residual Network to overcome the problems of learning with deeper network. The original paper is quite interesting. However for a gist you can follow the great article provided by Alex Smola in his course Dive into Deep Learning, Section 7.6. I am borrowing the content from there for easy understanding. The pytorch code is available in this github repo [chapter 9].
However another great tutorial is available from Sebastian Raschka in his github repo as well. This survey is a combination of all of them.
Residual Networks (ResNet)
Must Watch ![]()
* In case the above link is broken, click here
Must Watch ![]()
* In case the above link is broken, click here
As we design increasingly deeper networks it becomes imperative to understand how adding layers can increase the complexity and expressiveness of the network. Even more important is the ability to design networks where adding layers makes networks strictly more expressive rather than just different. To make some progress we need a bit of theory.
Function Classes
Consider $\mathcal{F}$, the class of functions that a specific network architecture (together with learning rates and other hyperparameter settings) can reach. That is, for all $f \in \mathcal{F}$ there exists some set of parameters $W$ that can be obtained through training on a suitable dataset. Let’s assume that $f^∗$ is the function that we really would like to find.
If it is in $\mathcal{F}$, we are in good shape but typically we will not be quite so lucky. Instead, we will try to find some $f^∗_{\mathcal{F}}$ which is our best bet within $\mathcal{F}$. For instance, we might try finding it by solving the following optimization problem:
It is only reasonable to assume that if we design a different and more powerful architecture $\mathcal{F}’$ we should arrive at a better outcome. In other words, we would expect that $f_{F’}^{\star}$ is better than $f_{F}^{\star}$. However, if
there is no guarantee that this should even happen. In fact, $f^{∗}_{\mathcal{F}’}$ might well be worse.
This is a situation that we often encounter in practice - adding layers does not only make the network more expressive, it also changes it in sometimes not quite so predictable ways. The following illustrates this in slightly abstract terms.
Fig. Left: non-nested function classes. The distance may in fact increase as the complexity increases. Right: with nested function classes this does not happen.
Only if larger function (right picture) classes contain the smaller ones are we guaranteed that increasing them strictly increases the expressive power of the network.
This is the question that He et al, 2016 considered when working on very deep computer vision models. At the heart of ResNet is the idea that every additional layer should contain the identity function as one of its elements. This means that if we can train the newly-added layer into an identity mapping $f(\mathbf{x})=\mathbf{x}$, the new model will be as effective as the original model. As the new model may get a better solution to fit the training dataset, the added layer might make it easier to reduce training errors. Even better, the identity function rather than the null $f(\mathbf{x})=0$ should be the simplest function within a layer.
Residual Blocks
- Let’s focus on a local neural network, as depicted below. Denote the input by $\mathbf{x}$. We assume that the ideal mapping we want to obtain by learning is $f(\mathbf{x})$, to be used as the input to the activation function.
- The portion within the dotted-line box in the
left imagemust directly fit the mapping $f(\mathbf{x})$. This can be tricky if we do not need that particular layer and we would much rather retain the input x. - The portion within the dotted-line box in the
right imagenow only needs to parametrize the deviation from the identity, since we return $\mathbf{x} + f(\mathbf{x})$. - In practice, the residual mapping is often easier to optimize. We only need to set $f(\mathbf{x})=0$. The right image in the below figure illustrates the basic Residual Block of
ResNet. Similar architectures were later proposed for sequence models which we will study later.
Fig. The difference between a regular block (left) and a residual block (right). In the latter case, we can short-circuit the convolutions.¶
- ResNet follows VGG’s full $3×3$ convolutional layer design. The residual block has two $3×3$ convolutional layers with the same number of output channels. Each convolutional layer is followed by a batch normalization layer and a ReLU activation function.
- Then, we skip these two convolution operations and add the input directly before the final ReLU activation function. This kind of design requires that the output of the two convolutional layers be of the same shape as the input, so that they can be added together. If we want to change the number of channels or the stride, we need to introduce an additional 1×1 convolutional layer to transform the input into the desired shape for the addition operation. Let’s have a look at the code below.
Implementation
pytorch implementation:
import sys
sys.path.insert(0, '..')
import d2l
import torch
import torch.nn as nn
import torch.nn.functional as F
# This class has been saved in the d2l package for future use
class Residual(nn.Module):
def __init__(self,input_channels, num_channels, use_1x1conv=False, strides=1, **kwargs):
super(Residual, self).__init__(**kwargs)
self.conv1 = nn.Conv2d(input_channels, num_channels,kernel_size=3, padding=1, stride=strides)
self.conv2 = nn.Conv2d(num_channels, num_channels, kernel_size=3, padding=1)
if use_1x1conv:
self.conv3 = nn.Conv2d(input_channels, num_channels, kernel_size=1, stride=strides)
else:
self.conv3 = None
self.bn1 = nn.BatchNorm2d(num_channels)
self.bn2 = nn.BatchNorm2d(num_channels)
self.relu = nn.ReLU(inplace=True)
def forward(self, X):
Y = self.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3:
X = self.conv3(X)
Y += X
Y =self.relu(Y)
return Y
This code generates two types of networks: one where we add the input to the output before applying the ReLU nonlinearity, and whenever use_1x1conv=True, one where we adjust channels and resolution by means of a 1×1 convolution before adding. The below figure illustrates this:
Implementation 2
However for another easy understanding we can follow the simple yet intuitive implementation in this notebook by Sebastian Raschka.
ResNet with identity blocks
The following code implements the residual blocks with skip connections such that the input passed via the shortcut matches the dimensions of the main path’s output, which allows the network to learn identity functions. Such a residual block is illustrated below:

##########################
### MODEL
##########################
class ConvNet(torch.nn.Module):
def __init__(self, num_classes):
super(ConvNet, self).__init__()
#########################
### 1st residual block
#########################
# 28x28x1 => 28x28x4
self.conv_1 = torch.nn.Conv2d(in_channels=1,
out_channels=4,
kernel_size=(1, 1),
stride=(1, 1),
padding=0)
self.conv_1_bn = torch.nn.BatchNorm2d(4)
# 28x28x4 => 28x28x1
self.conv_2 = torch.nn.Conv2d(in_channels=4,
out_channels=1,
kernel_size=(3, 3),
stride=(1, 1),
padding=1)
self.conv_2_bn = torch.nn.BatchNorm2d(1)
#########################
### 2nd residual block
#########################
# 28x28x1 => 28x28x4
self.conv_3 = torch.nn.Conv2d(in_channels=1,
out_channels=4,
kernel_size=(1, 1),
stride=(1, 1),
padding=0)
self.conv_3_bn = torch.nn.BatchNorm2d(4)
# 28x28x4 => 28x28x1
self.conv_4 = torch.nn.Conv2d(in_channels=4,
out_channels=1,
kernel_size=(3, 3),
stride=(1, 1),
padding=1)
self.conv_4_bn = torch.nn.BatchNorm2d(1)
#########################
### Fully connected
#########################
self.linear_1 = torch.nn.Linear(28*28*1, num_classes)
def forward(self, x):
#########################
### 1st residual block
#########################
shortcut = x
out = self.conv_1(x)
out = self.conv_1_bn(out)
out = F.relu(out)
out = self.conv_2(out)
out = self.conv_2_bn(out)
out += shortcut
out = F.relu(out)
#########################
### 2nd residual block
#########################
shortcut = out
out = self.conv_3(out)
out = self.conv_3_bn(out)
out = F.relu(out)
out = self.conv_4(out)
out = self.conv_4_bn(out)
out += shortcut
out = F.relu(out)
#########################
### Fully connected
#########################
logits = self.linear_1(out.view(-1, 28*28*1))
probas = F.softmax(logits, dim=1)
return logits, probas
torch.manual_seed(random_seed)
model = ConvNet(num_classes=num_classes)
model = model.to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
ResNet with convolutional blocks for resizing
The following code implements the residual blocks with skip connections such that the input passed via the shortcut matches is resized to dimensions of the main path’s output. Such a residual block is illustrated below:
##########################
### MODEL
##########################
class ConvNet(torch.nn.Module):
def __init__(self, num_classes):
super(ConvNet, self).__init__()
#########################
### 1st residual block
#########################
# 28x28x1 => 14x14x4
self.conv_1 = torch.nn.Conv2d(in_channels=1,
out_channels=4,
kernel_size=(3, 3),
stride=(2, 2),
padding=1)
self.conv_1_bn = torch.nn.BatchNorm2d(4)
# 14x14x4 => 14x14x8
self.conv_2 = torch.nn.Conv2d(in_channels=4,
out_channels=8,
kernel_size=(1, 1),
stride=(1, 1),
padding=0)
self.conv_2_bn = torch.nn.BatchNorm2d(8)
# 28x28x1 => 14x14x8
self.conv_shortcut_1 = torch.nn.Conv2d(in_channels=1,
out_channels=8,
kernel_size=(1, 1),
stride=(2, 2),
padding=0)
self.conv_shortcut_1_bn = torch.nn.BatchNorm2d(8)
#########################
### 2nd residual block
#########################
# 14x14x8 => 7x7x16
self.conv_3 = torch.nn.Conv2d(in_channels=8,
out_channels=16,
kernel_size=(3, 3),
stride=(2, 2),
padding=1)
self.conv_3_bn = torch.nn.BatchNorm2d(16)
# 7x7x16 => 7x7x32
self.conv_4 = torch.nn.Conv2d(in_channels=16,
out_channels=32,
kernel_size=(1, 1),
stride=(1, 1),
padding=0)
self.conv_4_bn = torch.nn.BatchNorm2d(32)
# 14x14x8 => 7x7x32
self.conv_shortcut_2 = torch.nn.Conv2d(in_channels=8,
out_channels=32,
kernel_size=(1, 1),
stride=(2, 2),
padding=0)
self.conv_shortcut_2_bn = torch.nn.BatchNorm2d(32)
#########################
### Fully connected
#########################
self.linear_1 = torch.nn.Linear(7*7*32, num_classes)
def forward(self, x):
#########################
### 1st residual block
#########################
shortcut = x
out = self.conv_1(x) # 28x28x1 => 14x14x4
out = self.conv_1_bn(out)
out = F.relu(out)
out = self.conv_2(out) # 14x14x4 => 714x14x8
out = self.conv_2_bn(out)
# match up dimensions using a linear function (no relu)
shortcut = self.conv_shortcut_1(shortcut)
shortcut = self.conv_shortcut_1_bn(shortcut)
out += shortcut
out = F.relu(out)
#########################
### 2nd residual block
#########################
shortcut = out
out = self.conv_3(out) # 14x14x8 => 7x7x16
out = self.conv_3_bn(out)
out = F.relu(out)
out = self.conv_4(out) # 7x7x16 => 7x7x32
out = self.conv_4_bn(out)
# match up dimensions using a linear function (no relu)
shortcut = self.conv_shortcut_2(shortcut)
shortcut = self.conv_shortcut_2_bn(shortcut)
out += shortcut
out = F.relu(out)
#########################
### Fully connected
#########################
logits = self.linear_1(out.view(-1, 7*7*32))
probas = F.softmax(logits, dim=1)
return logits, probas
torch.manual_seed(random_seed)
model = ConvNet(num_classes=num_classes)
model = model.to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
ResNet with convolutional blocks for resizing (using a helper class)
class ResidualBlock(torch.nn.Module):
def __init__(self, channels):
super(ResidualBlock, self).__init__()
self.conv_1 = torch.nn.Conv2d(in_channels=channels[0],
out_channels=channels[1],
kernel_size=(3, 3),
stride=(2, 2),
padding=1)
self.conv_1_bn = torch.nn.BatchNorm2d(channels[1])
self.conv_2 = torch.nn.Conv2d(in_channels=channels[1],
out_channels=channels[2],
kernel_size=(1, 1),
stride=(1, 1),
padding=0)
self.conv_2_bn = torch.nn.BatchNorm2d(channels[2])
self.conv_shortcut_1 = torch.nn.Conv2d(in_channels=channels[0],
out_channels=channels[2],
kernel_size=(1, 1),
stride=(2, 2),
padding=0)
self.conv_shortcut_1_bn = torch.nn.BatchNorm2d(channels[2])
def forward(self, x):
shortcut = x
out = self.conv_1(x)
out = self.conv_1_bn(out)
out = F.relu(out)
out = self.conv_2(out)
out = self.conv_2_bn(out)
# match up dimensions using a linear function (no relu)
shortcut = self.conv_shortcut_1(shortcut)
shortcut = self.conv_shortcut_1_bn(shortcut)
out += shortcut
out = F.relu(out)
return out
##########################
### MODEL
##########################
class ConvNet(torch.nn.Module):
def __init__(self, num_classes):
super(ConvNet, self).__init__()
self.residual_block_1 = ResidualBlock(channels=[1, 4, 8])
self.residual_block_2 = ResidualBlock(channels=[8, 16, 32])
self.linear_1 = torch.nn.Linear(7*7*32, num_classes)
def forward(self, x):
out = self.residual_block_1.forward(x)
out = self.residual_block_2.forward(out)
logits = self.linear_1(out.view(-1, 7*7*32))
probas = F.softmax(logits, dim=1)
return logits, probas
torch.manual_seed(random_seed)
model = ConvNet(num_classes=num_classes)
model.to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
Reference:
- ResNet-with-convolutional-blocks by Sebastian Raschka
- Dive into DL by Alex Smola
- Pytorch code for Dive into DL
Why it’s called Residual Network?
Where is the residue? It’s time we let the mathematicians within us to come to the surface. Let us consider a neural network block, whose input is $x$ and we would like to learn the true distribution $H(x)$. Let us denote the difference (or the residual) between this as
Rearranging it, we get,
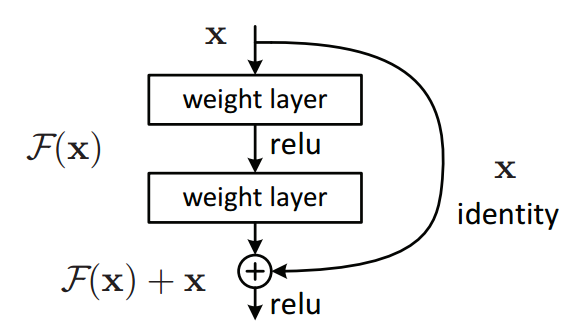
Our residual block is overall trying to learn the true output, $H(x)$ and if you look closely at the image above, you will realize that since we have an identity connection coming due to $x$, the layers are actually trying to learn the residual, $R(x)$.
So to summarize, the layers in a traditional network are learning the true output $(H(x))$ whereas the layers in a residual network are learning the residual $(R(x))$. Hence, the name: Residual Block.
It has also been observed that it is easier to learn residual of output and input, rather than only the input.
As an added advantage, our network can now learn identity function by simply setting residual as zero. And if you truly understand backpropagation and how severe the problem of vanishing gradient becomes with increasing number of layers, then you can clearly see that because of these skip connections, we can propagate larger gradients to initial layers and these layers also could learn as fast as the final layers, giving us the ability to train deeper networks. The image below shows how we can arrange the residual block and identity connections for the optimal gradient flow. It has been observed that pre-activations with batch normalizations give the best results in general (i.e. the right-most residual block in the image below gives most promising results).

The image below shows multiple interpretations of a residual block.

History of skip connections.
The idea of skipping connections between the layers was first introduced in Highway Networks. Highway networks had skip connections with gates that
- controlled how much information is passed through them
- these gates can be trained to open selectively.
This idea is also seen in the LSTM networks that control how much information flows from the past data points seen by the network. These gates work similar to control of memory flow from the previously seen data points. Same idea is shown in the image below.

Residual blocks are basically a special case of highway networks without any gates in their skip connections.
Essentially, residual blocks allows the flow of memory (or information) from initial layers to last layers. Despite the absence of gates in their skip connections, residual networks perform as good as any other highway network in practice. And before ending this article, below is an image of how the collection of all residual blocks completes into a ResNet .

For more details read this very good blog.
Reference: