Deep Learning Concepts (Part 1)

Content

  1. Content
  2. Deep Learning - Design Decision
  3. Gradient Decent
    1. Batch gradient descent
    2. Stochastic gradient descent:
    3. Mini-batch gradient descent
    4. Momentum
    5. Adam
    6. Batch normalization
  4. Compare stochastic gradient descent to interior point methods
  5. How Stochastic Gradient Decent with momentum works?
  6. How are kernel methods different from Neural Network?
  7. Statistical view of Deep Learning
  8. How are neural nets related to Fourier transforms?
  9. What is the best practice of avoiding the vanishing gradient problems with deep networks?
  10. A few QA’s from Kyunghyun Cho :fire:
  11. How to apply embedding for categorical variable?
    1. Model Architecture

Deep Learning - Design Decision

Gradient Decent

The main idea is that the sign of the derivative of the function at a specific value of x tells you if you need to increase (if negative slope) or decrease (if positive slope) x to reach the minimum. When the slope is near 0, the minimum should have been reached. (Minimizing Function)

There are three variants of gradient descent, which differ in how much data we use to compute the gradient of the objective function. Depending on the amount of data, we make a trade-off between the accuracy of the parameter update and the time it takes to perform an update.

Batch gradient descent

Vanilla gradient descent, aka batch gradient descent, computes the gradient of the cost function w.r.t. to the parameters θ for the entire training dataset:

$\theta = \theta - \eta \cdot \nabla_\theta J( \theta)$

As we need to calculate the gradients for the whole dataset to perform just one update, batch gradient descent can be very slow and is intractable for datasets that don’t fit in memory.

for i in range(nb_epochs):
  params_grad = evaluate_gradient(loss_function, data, params)
  params = params - learning_rate * params_grad

Stochastic gradient descent:

Stochastic gradient descent (SGD) in contrast performs a parameter update for each training example $x^{(i)}$ and label $y^{(i)}$:

$\theta = \theta - \eta \cdot \nabla_\theta J( \theta; x^{(i)}; y^{(i)})$

Batch gradient descent performs redundant computations for large datasets, as it recomputes gradients for similar examples before each parameter update. SGD does away with this redundancy by performing one update at a time. It is therefore usually much faster and can also be used to learn online.

for i in range(nb_epochs):
  np.random.shuffle(data)
  for example in data:
    params_grad = evaluate_gradient(loss_function, example, params)
    params = params - learning_rate * params_grad

Mini-batch gradient descent

Mini-batch gradient descent finally takes the best of both worlds and performs an update for every mini-batch of n training examples:

$\theta = \theta - \eta \cdot \nabla_\theta J( \theta; x^{(i:i+n)}; y^{(i:i+n)})$ 
for i in range(nb_epochs):
  np.random.shuffle(data)
  for batch in get_batches(data, batch_size=50):
    params_grad = evaluate_gradient(loss_function, batch, params)
    params = params - learning_rate * params_grad

Momentum

LEFT: shows a long shallow ravine leading to the optimum and steep walls on the sides. Standard SGD will tend to oscillate across the narrow ravine. RIGHT: Momentum is one method for pushing the objective more quickly along the shallow ravine.

![image](https://st4.ning.com/topology/rest/1.0/file/get/3713179836?profile=RESIZE_710x)

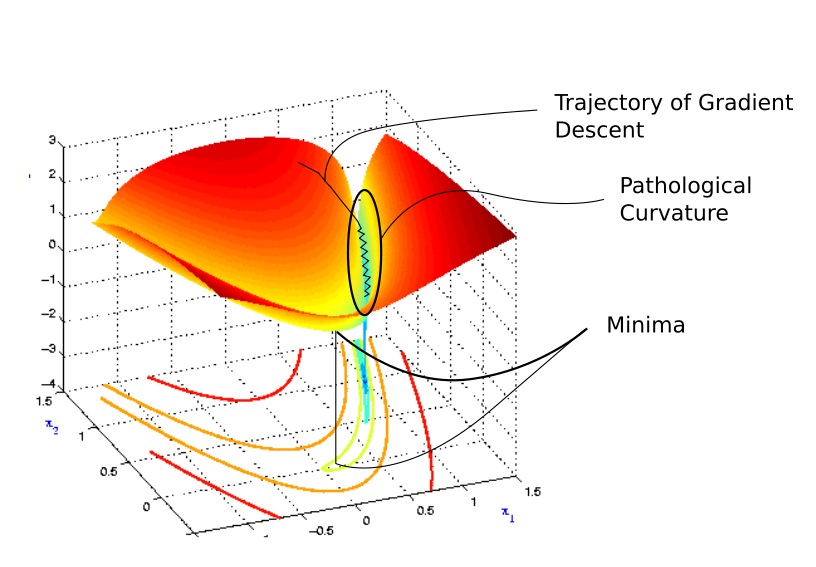
SGD has trouble navigating ravines, i.e. areas where the surface curves much more steeply in one dimension than in another, which are common around local optima. In these scenarios, SGD oscillates across the slopes of the ravine while only making hesitant progress along the bottom towards the local optimum.

Momentum is a method that helps accelerate SGD in the relevant direction and dampens oscillations. It does this by adding a fraction $\gamma$ of the update vector of the past time step to the current update vector:

$v_t = \gamma v_{t-1} + \eta \nabla_\theta J( \theta)$
$\theta = \theta - v_t$

Essentially, when using momentum, we push a ball down a hill. The ball accumulates momentum as it rolls downhill, becoming faster and faster on the way (until it reaches its terminal velocity if there is air resistance, i.e. γ<1). The same thing happens to our parameter updates: The momentum term increases for dimensions whose gradients point in the same directions and reduces updates for dimensions whose gradients change directions. As a result, we gain faster convergence and reduced oscillation.

Adam

Adaptive Moment Estimation (Adam) is another method that computes adaptive learning rates for each parameter. In stores the below 2 things

  1. Exponentially decaying average of past squared gradients $v_t$ like Adadelta and RMSprop ($2^{nd}$ moment of gradient),
$v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2$
  1. Exponentially decaying average of past gradients $m_t$, similar to momentum, ($1^{st}$ moment of gradient).
$m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t$

:radio_button: Physical Intuition: Momentum can be seen as a ball running down a slope, Adam behaves like a heavy ball with friction, which thus prefers flat minima in the error surface.

$m_t$ and $v_t$ are estimates of the first moment (the mean) and the second moment (the un-centered variance) of the gradients respectively, hence the name of the method.

As $m_t$ and $v_t$ are initialized as vectors of $0$’s, the authors of Adam observe that they are biased towards zero, especially during the initial time steps, and especially when the decay rates are small (i.e. $\beta_1$ and $\beta_2$ are close to 1).

They counteract these biases by computing bias-corrected first and second moment estimates:

$\hat{m}_t = \dfrac{m_t}{1 - \beta^t_1}$
$\hat{v}_t = \dfrac{v_t}{1 - \beta^t_2}$

Finally combining all together here is the param update rule:

$ \theta_{t+1} = \theta_{t} - \dfrac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t $

The authors propose default values of $0.9$ for $\beta_1$, $0.999$ for $\beta_2$, and $10^{-8}$ for $\epsilon$. They show empirically that Adam works well in practice and compares favorably to other adaptive learning-method algorithms.

Batch normalization

To facilitate learning, we typically normalize the initial values of our parameters by initializing them with zero mean and unit variance. As training progresses and we update parameters to different extents, we lose this normalization, which slows down training and amplifies changes as the network becomes deeper.

Batch normalization reestablishes these normalizations for every mini-batch and changes are back-propagated through the operation as well.

By making normalization part of the model architecture, we are able to use higher learning rates and pay less attention to the initialization parameters. Batch normalization additionally acts as a regularizer, reducing (and sometimes even eliminating) the need for Dropout.

For more details look here.

Reference:

Content

Compare stochastic gradient descent to interior point methods

Content

How Stochastic Gradient Decent with momentum works?

  • An SGD can be thought of as a ball rolling down the hill where the velocity of the ball is influenced by the gradient of the curve. However, in this approach, the ball has a chance to get stuck in any ravine. So if the ball can have enough momentum to get past get past the ravine would have been better. based on this idea, SGD with Momentum works. Where the ball has been given some added momentum which is based on the previous velocity and gradient.
    • velocity = momentum*past_velocity + learning_rate*gradient
    • w=w-velocity
    • past_velocity = velocity
  • easy explanation
  • book: deep learning in Python - by Cholet, page 51, but the equation looks suspicious
  • through explanation, distill pub

Content

How are kernel methods different from Neural Network?

they are more than simply related, they are duals of each other ~Shakir M

One way to think about an NN with L layers is that the first L - 1 layers perform some non-linear transformation $\phi(x_i;\theta)$ on the input data point $x_i$ parameterized by $\theta$, while the last layer is just a linear model on these non-linear representations parameterized by a weights vector $w$.

It can be shown that some class of NN models is mathematically equivalent to a kernelized ridge-regression model. Further steps in the back-propagation adjust the parameters $\theta$ of the non-linear transformation $\phi$, which has the effect of adjusting the equivalent kernel matrix at the $t$ step of the next iteration of back-propagation. So it could be said that this class of NNs is mathematically equivalent to a kernelized ridge-regression that learns its own kernel from the data. Of course, these NNs are only able to learn kernels in finite-dimensional spaces, unlike the kernel based-methods which can use kernels in infinite-dimensional spaces. For full math details check the below blogs.

Reference:

Content

Statistical view of Deep Learning

In deep learning, the link function is referred to as the activation function

Content

How are neural nets related to Fourier transforms?

What are Fourier transforms, for that matter?

Content

What is the best practice of avoiding the vanishing gradient problems with deep networks?

The vanishing gradient problem occurs because of the use of chain rule for backpropagation, and the fact that traditional activation functions (𝑡𝑎𝑛ℎ and sigmoid) produce values with magnitude less than 1. So people use the following solutions:

  • As Daniel Lindsäth has said, use ReLU neurons as activation function
  • Combine careful initialization of weights (such that they are not initialized in the saturation region of the activation function) with small learning rates
  • Batch Normalization, where they employ an adaptive and learned normalization scheme to force the activations of a layer the follow a single distribution, independent of the changes in the parameters of upstream layers (Accelerating Deep Network Training by Reducing Internal Covariate Shift )

Reference:

Content

A few QA’s from Kyunghyun Cho :fire:

How to apply embedding for categorical variable?

image

Model Architecture

The first layer of the network contains embeddings for each categorical feature. These are initialized randomly, but updated via gradient descent through training. Embeddings are then concatenated and passed through a fully connected layer that fans out to an output layer that is the same size as the number of retailers we have. This is followed by a sigmoid activation due to the nature of the multi-label classification task.

image

Unlike most models where we’re interested in the outputs, in this case, we’re interested in the inputs. More precisely, we’re trying to extract the learned representation of the inputs in the embedding layer of the network. We can easily extract these from the weights of the neural network within the state_dict() of the trained model.

Results

One of the most interesting applications of the resulting embeddings is to examine the distance between different categories within this new latent space using a standard similarity score like cosine similarity. Take state for example — since we used retailer prediction as the supervised task to train these embeddings and retailers are sometimes regional, we might expect geographically close states to have similar embeddings. We can confirm this by selecting some example states and looking at their top 5 nearest neighbors by cosine similarity.

image

:paperclip: Reference:

Back to Top

Published on July 16, 2019